【题目】定义:若某抛物线上有两点A、B关于原点对称,则称该抛物线为“完美抛物线”.已知二次函数y=ax2﹣2mx+c(a,m,c均为常数且ac≠0)是“完美抛物线”:
(1)试判断ac的符号;
(2)若c=﹣1,该二次函数图象与y轴交于点C,且S△ABC=1.
①求a的值;
②当该二次函数图象与端点为M(﹣1,1)、N(3,4)的线段有且只有一个交点时,求m的取值范围.
参考答案:
【答案】
(1)
解:设A (p,q).则B (﹣p,﹣q),
把A、B坐标代入解析式可得: ![]() ,
,
∴2ap2+2c=0.即 ![]() ,
,
∴ ![]() ,
,
∵ac≠0,
∴ ![]() ,
,
∴ac<0
(2)
解:∵c=﹣1,
∴ ![]() ,a>0,且C(0,﹣1),
,a>0,且C(0,﹣1),
∴ ![]() ,
,
①S△ABC= ![]() ×2
×2 ![]() ×1=1,
×1=1,
∴a=1;
②由①可知:抛物线解析式为y=x2﹣2mx﹣1,
∵M(﹣1,1)、N(3,4).
∴MN: ![]() (﹣1≤x≤3),
(﹣1≤x≤3),
依题,只需联立 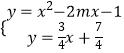 在﹣1≤x≤3内只有一个解即可,
在﹣1≤x≤3内只有一个解即可,
∴x2﹣2mx﹣1= ![]() x+
x+ ![]() ,
,
故问题转化为:方程x2﹣(2m+ ![]() )x﹣
)x﹣ ![]() =0在﹣1≤x≤3内只有一个解,
=0在﹣1≤x≤3内只有一个解,
建立新的二次函数:y=x2﹣(2m+ ![]() )x﹣
)x﹣ ![]() ,
,
∵△=(2m+ ![]() )2+11>0且c=﹣
)2+11>0且c=﹣ ![]() <0,
<0,
∴抛物线 ![]() 与x轴有两个交点,且交y轴于负半轴.
与x轴有两个交点,且交y轴于负半轴.
不妨设方程 ![]() 的两根分别为x1,x2.(x1<x2)
的两根分别为x1,x2.(x1<x2)
则 ![]()
∵方程 ![]() 在﹣1≤x≤3内只有一个解.
在﹣1≤x≤3内只有一个解.
故分两种情况讨论:
(Ⅰ)若﹣1≤x1<3且x2>3:则 ![]() .即:
.即: ![]() ,
,
可得: ![]() .
.
(Ⅱ)若x1<﹣1且﹣1<x2≤3:则 ![]() .即:
.即: ![]() ,
,
可得: ![]() ,
,
综上所述, ![]() 或
或 ![]()
【解析】(1)设A (p,q).则B (﹣p,﹣q),把A、B坐标代入解析式可得方程组即可得到结论;(2)由c=﹣1,得到 ![]() ,a>0,且C(0,﹣1),求得
,a>0,且C(0,﹣1),求得 ![]() ,①根据三角形的面积公式列方程即可得到结果;②由①可知:抛物线解析式为y=x2﹣2mx﹣1,根据M(﹣1,1)、N(3,4).得到这些MN的解析式
,①根据三角形的面积公式列方程即可得到结果;②由①可知:抛物线解析式为y=x2﹣2mx﹣1,根据M(﹣1,1)、N(3,4).得到这些MN的解析式 ![]() (﹣1≤x≤3),联立方程组得到x2﹣2mx﹣1=
(﹣1≤x≤3),联立方程组得到x2﹣2mx﹣1= ![]() x+
x+ ![]() ,故问题转化为:方程x2﹣(2m+
,故问题转化为:方程x2﹣(2m+ ![]() )x﹣
)x﹣ ![]() =0在﹣1≤x≤3内只有一个解,建立新的二次函数:y=x2﹣(2m+
=0在﹣1≤x≤3内只有一个解,建立新的二次函数:y=x2﹣(2m+ ![]() )x﹣
)x﹣ ![]() ,根据题意得到(Ⅰ)若﹣1≤x1<3且x2>3,(Ⅱ)若x1<﹣1且﹣1<x2≤3:列方程组即可得到结论.
,根据题意得到(Ⅰ)若﹣1≤x1<3且x2>3,(Ⅱ)若x1<﹣1且﹣1<x2≤3:列方程组即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A、B在坐标轴上,其中A(0,a)、B(b,0)满足:|2a﹣b﹣1|+
 =0.
=0.(1)求A、B两点的坐标;
(2)将线段AB平移到CD,点A的对应点为C(﹣2,t),如图1所示.若三角形ABC的面积为9,求点D的坐标;
(3)平移线段AB到CD,若点C、D也在坐标轴上,如图2所示,P为线段AB上的一动点(不与A、B重合),连接OP,PE平分∠OPB,∠BCE=2∠ECD.求证:∠BCD=3(∠CEP﹣∠OPE).

-
科目: 来源: 题型:
查看答案和解析>>【题目】一天,某客运公司的甲、乙两辆客车分别从相距380千米的A、B两地同时出发相向而行,并以各自的速度匀速行驶,两车行驶2小时时甲车先到达服务区C地,此时两车相距20千米,甲车在服务区C地休息了20分钟,然后按原速度开往B地;乙车行驶2小时15分钟时也经过C地,未停留继续开往A地.(友情提醒:画出线段图帮助分析)
(1)乙车的速度是________千米/小时,B、C两地的距离是________千米, A、C两地的距离是________千米;
(2)求甲车的速度;
(3)这一天,乙车出发多长时间,两车相距200千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=4,AD=6,M是AD边的中点,P是射线AB上的一个动点(不与A,B重合),MN⊥PM交射线BC于N点.

(1)如图1,当点N与点C重合时,求AP的长;
(2)如图2,在点N的运动过程中,求证: 为定值;
为定值;
(3)在射线AB上,是否存在点P,使得△DCN∽△PMN?若存在,求此时AP的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(徐州中考)如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长交DC于点F,求证:
(1)△ABE≌△CFE;
(2)四边形ABFD是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
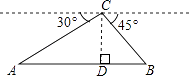
A.200米
B.200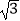 米
米
C.220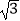 米
米
D.100(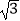 +1)米
+1)米
相关试题

