【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向向右平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 . 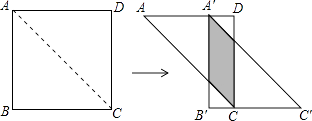
参考答案:
【答案】4或8
【解析】解:设AC交A′B′于H,

∵A′H∥CD,AC∥CA′,
∴四边形A′HCD是平行四边形,
∵∠A=45°,∠D=90°
∴△A′HA是等腰直角三角形
设AA′=x,则阴影部分的底长为x,高A′D=12﹣x
∴x(12﹣x)=32
∴x=4或8,
即AA′=4或8cm.
所以答案是:4或8.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分,以及对平移的性质的理解,了解①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
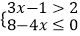 的解集在数轴上表示为( )
的解集在数轴上表示为( )
A.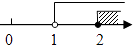
B.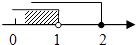
C.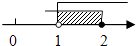
D.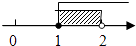
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子里,有5个除颜色外,其他都相同的小球,其中有3个是红球,2个是绿球,每次拿一个球然后放回去,拿2次,则至少有一次取到绿球的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF , 其中正确的是( )
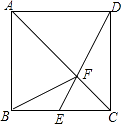
A.①③
B.②③
C.①④
D.②④ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点F是等边△ABC边CA延长线上一点,点D是线段BF上一点,且BC=CD,CD交AB于点E,若AE=6,CE=14,则AF= .
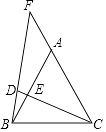
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:我们在学习二次根式时,式子
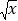 有意义,则x≥0;式子
有意义,则x≥0;式子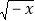 有意义,则x≤0;若式子
有意义,则x≤0;若式子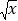 +
+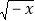 有意义,求x的取值范围. 这个问题可以转化为不等式组来解决,即求关于x的不等式组x≥0,x≤0的解集,解这个不等式组,得x=0. 请你运用上述的数学方法解决下列问题:
有意义,求x的取值范围. 这个问题可以转化为不等式组来解决,即求关于x的不等式组x≥0,x≤0的解集,解这个不等式组,得x=0. 请你运用上述的数学方法解决下列问题:(1)式子
 +
+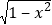 有意义,求x的取值范围;
有意义,求x的取值范围;(2)已知y=
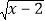 +
+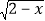 -3,求
-3,求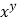 的值.
的值. -
科目: 来源: 题型:
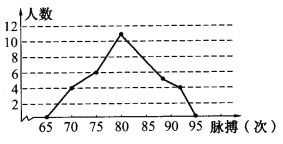
查看答案和解析>>【题目】下图示为若干名学生每分钟脉搏跳动次数的频数分布折线.
(1)求学生的总人数;
(2)分布在两端虚设的两组的组中值分别是多少?
(3)估计样本的中位数.
相关试题

