【题目】如图1,△ACB为等腰三角形,∠ABC=90°,点P在线段BC上(不与B,C重合),以AP为腰长作等腰直角△PAQ,QE⊥AB于E.

(1)求证:△PAB≌△AQE;
(2)连接CQ交AB于M,若PC=2PB,求![]() 的值;
的值;
(3)如图2,过Q作QF⊥AQ交AB的延长线于点F,过P点作DP⊥AP交AC于D,连接DF,当点P在线段BC上运动时(不与B,C重合),式子![]() 的值会变化吗?若不变,求出该值;若变化,请说明理由.
的值会变化吗?若不变,求出该值;若变化,请说明理由.
参考答案:
【答案】(1)证明见解析;(2)2;(3)不会变化.值为1.
【解析】试题分析:(1)根据题目中的信息可以得到AQ=AP,∠QEA与∠ABP之间的关系,∠QAE与∠APB之间的关系,从而可以解答本题;
(2)由第一问中的两个三角形全等,可以得到各边之间的关系,然后根据题目中的信息找到PC与MB的关系,从而可以解答本题;
(3)作合适的辅助线,构造直角三角形,通过三角形的全等可以找到所求问题需要的边之间的关系,从而可以解答本题.
试题解析:(1)证明:∵△ACB为等腰三角形,∠ABC=90°,点P在线段BC上(不与B,C重合),以AP为腰长作等腰直角△PAQ,QE⊥AB于E.
∴AP=AQ,∠ABP=∠QEA=90°,∠QAE+∠BAP=∠BAP+∠APB=90°,
∴∠QAE=∠APB,
在△PAB和△AQE中,
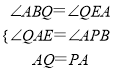 ,
,
∴△PAB≌△AQE(AAS);
(2)∵△PAB≌△AQE,
∴AE=PB,
∵AB=CB,
∴QE=CB.
在△QEM和△CBM中,
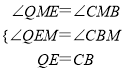 ,
,
∴△QEM≌△CBM(AAS),
∴ME=MB,
∵AB=CB,AE=PB,PC=2PB,
∴BE=PC,
∵PC=2PB,
∴PC=2MB,
∴![]() =2;
=2;
(3)式子![]() 的值不会变化.
的值不会变化.
如下图2所示:作HA⊥AC交QF于点H,

∵QA⊥AP,HA⊥AC,AP⊥PD,
∴∠QAH+∠HAP=∠HAP+∠PAD=90°,∠AQH=∠APD=90°,
∴∠QAH=∠PAD,
∵△PAQ为等腰直角三角形,
∴AQ=AP,
在△AQH和△APD中,
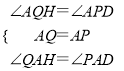 ,
,
∴△AQH≌△APD(ASA),
∴AH=AD,QH=PD,
∵HA⊥AC,∠BAC=45°,
∴∠HAF=∠DAF,
在△AHF和△ADF中,
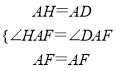 ,
,
∴△AHF≌△ADF(SAS),
∴HF=DF,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:2(3a2b﹣2ab2)﹣3(﹣ab2+3a2b),其中|a﹣1|+(b+2)2=0.
-
科目: 来源: 题型:
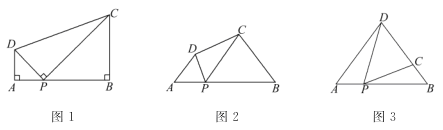
查看答案和解析>>【题目】 (1)、问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.求证:AD·BC=AP·BP.
(2)、探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)、应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,由点A 出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当DC的长与△ABD底边上的高相等时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 最小的有理数是0 B. 最小的正整数为0
C. 绝对值最小的负数为﹣1 D. 绝对值最小的有理数是0
-
科目: 来源: 题型:
查看答案和解析>>【题目】小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x是多少时,矩形场地面积S最大,最大面积是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】将命题“三条边对应相等的两个三角形全等”,改写成“如果…,那么…”的形式为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,△ABC的顶点A(-3,0)、B(0,3),AD⊥BC交BC于D点,交y轴正半轴于点E(0,t)
(1)当t=1时,求C点的坐标;
(2)如图2,求∠ADO的度数;
(3)如图3,已知点P(0,2),若PQ⊥PC,PQ=PC,求Q的坐标(用含t的式子表示).
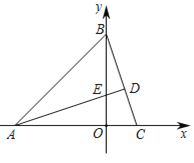
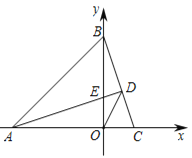
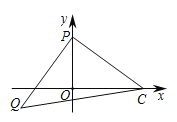
图1 图2 图3
相关试题

