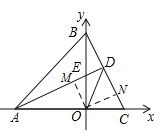
【题目】如图1,在平面直角坐标系中,△ABC的顶点A(-3,0)、B(0,3),AD⊥BC交BC于D点,交y轴正半轴于点E(0,t)
(1)当t=1时,求C点的坐标;
(2)如图2,求∠ADO的度数;
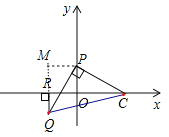
(3)如图3,已知点P(0,2),若PQ⊥PC,PQ=PC,求Q的坐标(用含t的式子表示).
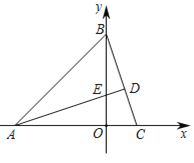
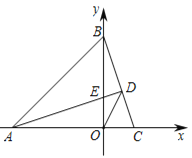
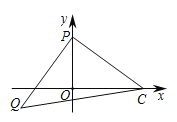
图1 图2 图3
参考答案:
【答案】(1)C(1,0);(2)∠ADO=45°;(3)Q(-2,2-t)
【解析】试题分析: ![]() 根据
根据![]() 得
得![]() ,即可求出点
,即可求出点![]() 坐标.
坐标.
![]() 先过点
先过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,根据
,根据![]() ,得到
,得到![]() ,且
,且![]() ,再根据
,再根据![]() 得出
得出![]() ,进而得到
,进而得到![]() 平分
平分![]() ,求出
,求出![]() 的度数.
的度数.
![]() 过点
过点![]() 作
作![]() 垂直于
垂直于![]() 轴于
轴于![]() ,作
,作![]() 于
于![]() ,如图,易得四边形
,如图,易得四边形![]() 为矩形,证明
为矩形,证明![]() ,则可利用
,则可利用![]() 证明
证明![]() 即可求出点
即可求出点![]() 坐标.
坐标.
试题解析: ![]()
![]() ,
,
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,
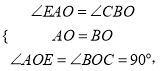
![]()
![]()
∴点![]() 坐标
坐标![]()
![]() 如图,过点
如图,过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,
,
![]()
![]() .
.
![]()
![]()
![]()
![]() 平分
平分![]() .
.
![]()
![]() 过点
过点![]() 作
作![]() 垂直于
垂直于![]() 轴于
轴于![]() ,作
,作![]() 于
于![]() ,
,
由![]() 知点
知点![]() 的坐标为:
的坐标为: ![]() .
.
四边形![]() 为矩形,
为矩形,
![]()
![]()
在![]() 和
和![]() 中
中
![]()
![]()
![]() 点
点![]() 坐标是
坐标是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ACB为等腰三角形,∠ABC=90°,点P在线段BC上(不与B,C重合),以AP为腰长作等腰直角△PAQ,QE⊥AB于E.

(1)求证:△PAB≌△AQE;
(2)连接CQ交AB于M,若PC=2PB,求
 的值;
的值;(3)如图2,过Q作QF⊥AQ交AB的延长线于点F,过P点作DP⊥AP交AC于D,连接DF,当点P在线段BC上运动时(不与B,C重合),式子
 的值会变化吗?若不变,求出该值;若变化,请说明理由.
的值会变化吗?若不变,求出该值;若变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x是多少时,矩形场地面积S最大,最大面积是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】将命题“三条边对应相等的两个三角形全等”,改写成“如果…,那么…”的形式为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某专业户要出售300只羊,现在市场上羊的价格为每千克11元,为了估计这300只羊能卖多少钱,试问:(1)对于上述问题你认为是用普查好还是抽样调查好?
(2)该专业户从中随机抽取了5只羊,称得它们的重量如下:(单位:千克)
26 31 32 36 37
①在这个问题中,总体、个体和样本各是什么?
②通过上述数据,你能估计出这300只羊约能卖得多少元钱吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据,如图是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:

(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少人?占被调查人数的百分比是多少?
-
科目: 来源: 题型:
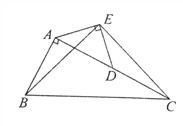
查看答案和解析>>【题目】如图在Rt△ABC中,∠BAC=90 o,AC=2AB,点D是AC的中点,将一块锐角为45 o的直角三角板如图放置,使三角板斜边的两个端点分别与A,D重合,连接BE,EC。试猜想线段BE和EC的数量及位置关系,并证明你的猜想。
相关试题

