搜索
【题目】小李想用篱笆围成一个周长为60米的矩形场地，矩形面积S（单位：平方米）随矩形一边长x（单位：米）的变化而变化．
（1）求S与x之间的函数关系式，并写出自变量x的取值范围；
（2）当x是多少时，矩形场地面积S最大，最大面积是多少？
参考答案：
【答案】
（1）解：S=x（30﹣x）
自变量x的取值范围为：
0＜x＜30
（2）解：S=x（30﹣x）
=﹣（x﹣15）2+225，
∴当x=15时，S有最大值为225平方米．
即当x是15时，矩形场地面积S最大，最大面积是225平方米
【解析】（1）已知周长为60米，一边长为x，则另一边长为30﹣x．（2）用配方法化简函数解析式，求出s的最大值．
-
科目： 来源： 题型：
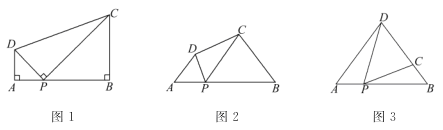
查看答案和解析>>【题目】 (1)、问题：如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°．求证：AD·BC=AP·BP．
(2)、探究：如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立？说明理由．
(3)、应用：请利用（1）（2）获得的经验解决问题：
如图3，在△ABD中，AB=6，AD=BD=5．点P以每秒1个单位长度的速度，由点A 出发，沿边AB向点B运动，且满足∠DPC=∠A．设点P的运动时间为t（秒），当DC的长与△ABD底边上的高相等时，求t的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是（ ）
A. 最小的有理数是0 B. 最小的正整数为0
C. 绝对值最小的负数为﹣1 D. 绝对值最小的有理数是0
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，△ACB为等腰三角形，∠ABC=90°，点P在线段BC上（不与B，C重合），以AP为腰长作等腰直角△PAQ，QE⊥AB于E．
（1）求证：△PAB≌△AQE；
（2）连接CQ交AB于M，若PC=2PB，求
的值；（3）如图2，过Q作QF⊥AQ交AB的延长线于点F，过P点作DP⊥AP交AC于D，连接DF，当点P在线段BC上运动时（不与B，C重合），式子
的值会变化吗？若不变，求出该值；若变化，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】将命题“三条边对应相等的两个三角形全等”，改写成“如果…，那么…”的形式为_____________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，△ABC的顶点A(－3，0)、B(0，3)，AD⊥BC交BC于D点，交y轴正半轴于点E(0，t)
（1）当t＝1时，求C点的坐标；
（2）如图2，求∠ADO的度数；
（3）如图3，已知点P(0，2)，若PQ⊥PC，PQ＝PC，求Q的坐标(用含t的式子表示)．
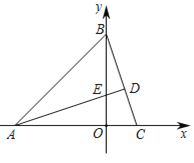
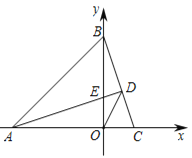
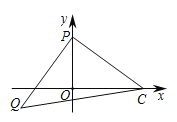
图1 图2 图3
-
科目： 来源： 题型：
查看答案和解析>>【题目】某专业户要出售300只羊，现在市场上羊的价格为每千克11元，为了估计这300只羊能卖多少钱，试问：（1）对于上述问题你认为是用普查好还是抽样调查好？
（2）该专业户从中随机抽取了5只羊，称得它们的重量如下：(单位：千克)
26 31 32 36 37
①在这个问题中，总体、个体和样本各是什么？
②通过上述数据，你能估计出这300只羊约能卖得多少元钱吗？
相关试题
