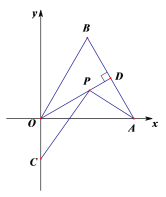
【题目】如图,在平面直角坐标系中,![]() OAB是边长为4的等边三角形,OD是AB边上的高,点P是OD上的一个动点,若点C的坐标是
OAB是边长为4的等边三角形,OD是AB边上的高,点P是OD上的一个动点,若点C的坐标是![]() ,则PA+PC的最小值是_________________.
,则PA+PC的最小值是_________________.
参考答案:
【答案】![]()
【解析】
由题意知,点A与点B关于直线OD对称,连接BC,则BC的长即为PC+AP的最小值,过点B作BN⊥y轴,垂足为N,过B作BM⊥x轴于M,求出BN、CN的长,然后利用勾股定理进行求解即可.
由题意知,点A与点B关于直线OD对称,连接BC,则BC的长即为PC+AP的最小值,
过点B作BN⊥y轴,垂足为N,过B作BM⊥x轴于M,则四边形OMBN是矩形,
∵△ABO是等边三角形,
∴OM=![]() AO=
AO=![]() ×4=2,∴BN=OM=2,
×4=2,∴BN=OM=2,
在Rt△OBM中,BM=![]() =
=![]() =2
=2![]() ,
,
∴ON=BM=2![]() ,
,
∵C![]() ,
,
∴CN=ON+OC=2![]() +
+![]() =3
=3![]() ,
,
在Rt△BNC中,BC=![]() ,
,
即PC+AP的最小值为![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在某市五个区投放共享单车供市民使用,投放量的分布及投放后的使用情况统计如下.
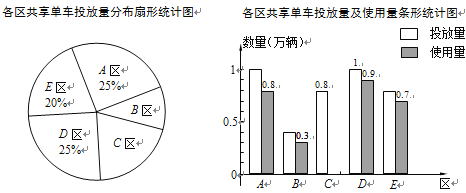
(1)该公司在全市一共投放了 万辆共享单车;
(2)在扇形统计图中,B区所对应扇形的圆心角为 °;
(3)该公司在全市投放的共享单车的使用量占投放量的85%,请计算C区共享单车的使用量并补全条形统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在直角坐标系中,A(﹣2,4)B(﹣4,2);A1、B1是A、B关于y轴的对称点;
(1)请在图中画出A、B关于原点O的对称点A2,B2(保留痕迹,不写作法);并直接写出A1、A2、B1、B2的坐标.
(2)试问:在x轴上是否存在一点C,使△A1B1C的周长最小,若存在求C点的坐标,若不存在说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ABC中,∠ACB=90°,∠ABC=22.5°,将
ABC中,∠ACB=90°,∠ABC=22.5°,将 ABC 绕着点C顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,连接BE.下列说法中,正确的有( )
ABC 绕着点C顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,连接BE.下列说法中,正确的有( )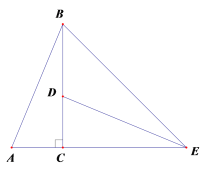
①DE⊥AB ②∠BCE是旋转角 ③∠BED=30° ④
 BDE与
BDE与 CDE面积之比是
CDE面积之比是 :1
:1A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,
 ABC的顶点均在格点上.
ABC的顶点均在格点上.(1)先将
 ABC向上平移4个单位后得到的
ABC向上平移4个单位后得到的 A1B1C1,再将
A1B1C1,再将 A1B1C1绕点C1按顺时针方向旋转90°后所得到的
A1B1C1绕点C1按顺时针方向旋转90°后所得到的 A2B2 C1,在图中画出
A2B2 C1,在图中画出 A1B1C1和
A1B1C1和 A2B2 C1.
A2B2 C1.(2)
 A2B2 C1能由
A2B2 C1能由 ABC绕着点O旋转得到,请在网格上标出点O.
ABC绕着点O旋转得到,请在网格上标出点O.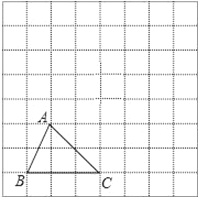
-
科目: 来源: 题型:
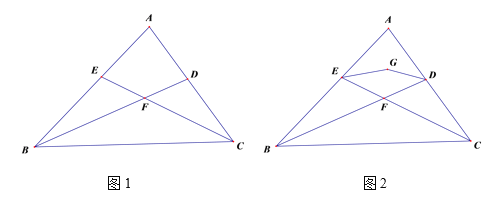
查看答案和解析>>【题目】如图1,在
 ABC中,∠A=80°,BD、CE分别平分∠ABC、∠ACB,BD与CE交于点F.
ABC中,∠A=80°,BD、CE分别平分∠ABC、∠ACB,BD与CE交于点F. (1)求∠BFC的度数;
(2)如图2,EG、DG分别平分∠AEF、∠ADF, EG与DG交于点G ,求∠EGD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.
(1)写出点Q的坐标是________;
(2)若把点Q向右平移
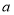 个单位长度,向下平移
个单位长度,向下平移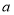 个单位长度后,得到的点
个单位长度后,得到的点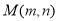 落在第四象限,求
落在第四象限,求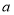 的取值范围;
的取值范围;(3)在(2)条件下,当
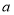 取何值,代数式
取何值,代数式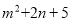 取得最小值.
取得最小值.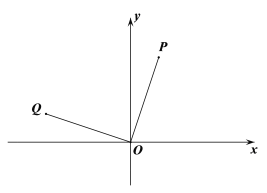
相关试题

