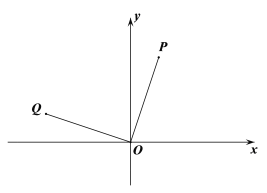
【题目】如图所示,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.
(1)写出点Q的坐标是________;
(2)若把点Q向右平移![]() 个单位长度,向下平移
个单位长度,向下平移![]() 个单位长度后,得到的点
个单位长度后,得到的点![]() 落在第四象限,求
落在第四象限,求![]() 的取值范围;
的取值范围;
(3)在(2)条件下,当![]() 取何值,代数式
取何值,代数式![]() 取得最小值.
取得最小值.
参考答案:
【答案】(1)Q(-3,1)(2)a>3(3)0
【解析】
(1)如图,作PA⊥x轴于A,QB⊥x轴于B,则∠PAO=∠OBQ=90°,证明△OBQ≌△PAO(AAS),从而可得OB=PA,QB=OA,继而根据点P的坐标即可求得答案;
(2)利用点平移的规律表示出Q′点的坐标,然后根据第四象限点的坐标特征得到a的不等式组,再解不等式即可;
(3)由(2)得,m=-3+a,n=1-a,代入所求式子得![]()
![]() ,继而根据偶次方的非负性即可求得答案 .
,继而根据偶次方的非负性即可求得答案 .
(1)如图,作PM⊥x轴于A,QN⊥x轴于B,则∠PAO=∠OBQ=90°,
∴∠P+∠POA=90°,
由旋转的性质得:∠POQ=90°,OQ=OP,
∴∠QOB+∠POA=90°,
∴∠QOB=∠P,
∴△OBQ≌△PAO(AAS),
∴OB=PA,QB=OA,
∵点P的坐标为(1,3),
∴OB=PA=3,QB=OA=1,
∴点Q的坐标为(-3,1);
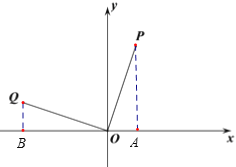
(2)把点Q(-3,1)向右平移a个单位长度,向下平移a个单位长度后,
得到的点M的坐标为(-3+a,1-a),
而M在第四象限,
所以![]() ,
,
解得a>3,
即a的范围为a>3;
(3)由(2)得,m=-3+a,n=1-a,
∴![]()
![]()
![]()
![]() ,
,
∵![]() ,
,
∴当a=4时,代数式![]() 的最小值为0.
的最小值为0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 OAB是边长为4的等边三角形,OD是AB边上的高,点P是OD上的一个动点,若点C的坐标是
OAB是边长为4的等边三角形,OD是AB边上的高,点P是OD上的一个动点,若点C的坐标是 ,则PA+PC的最小值是_________________.
,则PA+PC的最小值是_________________.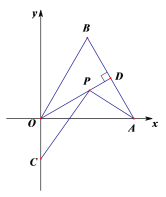
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,
 ABC的顶点均在格点上.
ABC的顶点均在格点上.(1)先将
 ABC向上平移4个单位后得到的
ABC向上平移4个单位后得到的 A1B1C1,再将
A1B1C1,再将 A1B1C1绕点C1按顺时针方向旋转90°后所得到的
A1B1C1绕点C1按顺时针方向旋转90°后所得到的 A2B2 C1,在图中画出
A2B2 C1,在图中画出 A1B1C1和
A1B1C1和 A2B2 C1.
A2B2 C1.(2)
 A2B2 C1能由
A2B2 C1能由 ABC绕着点O旋转得到,请在网格上标出点O.
ABC绕着点O旋转得到,请在网格上标出点O.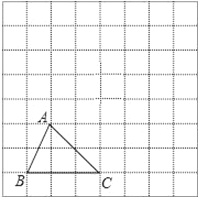
-
科目: 来源: 题型:
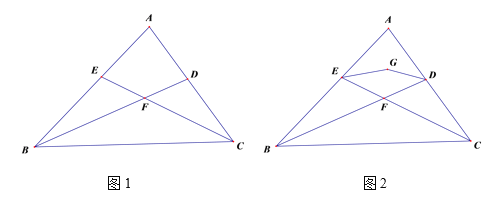
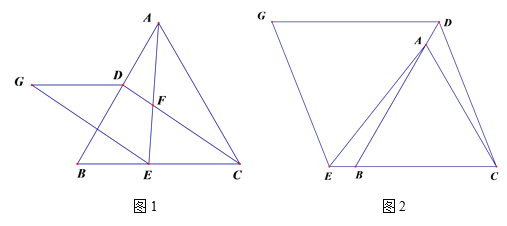
查看答案和解析>>【题目】如图1,在
 ABC中,∠A=80°,BD、CE分别平分∠ABC、∠ACB,BD与CE交于点F.
ABC中,∠A=80°,BD、CE分别平分∠ABC、∠ACB,BD与CE交于点F. (1)求∠BFC的度数;
(2)如图2,EG、DG分别平分∠AEF、∠ADF, EG与DG交于点G ,求∠EGD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
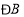 ,
,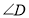 的两边分别平行.
的两边分别平行.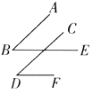
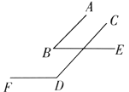
① ②
(1)在图①中,
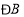 与
与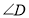 的数量关系是什么?为什么?
的数量关系是什么?为什么?(2)在图②中,
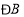 与
与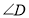 的数量关系是什么?为什么?
的数量关系是什么?为什么?(3)由(1)(2)可得结论:________;
(4)应用:若两个角的两边两两互相平行,其中一个角比另一个角的2倍少
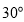 ,求这两个角的度数.
,求这两个角的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
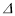 ABC为等边三角形,点D、E分别在直线AB、BC上,且AD=BE.
ABC为等边三角形,点D、E分别在直线AB、BC上,且AD=BE. (1)如图1,若点D、E分别是AB、CB边上的点,连接AE、CD交于点F,过点E作∠AEG=60°,使EG=AE,连接GD,则∠AFD= (填度数);
(2)在(1)的条件下,猜想DG与CE存在什么关系,并证明;
(3)如图2,若点D、E分别是BA、CB延长线上的点,(2)中结论是否仍然成立?请给出判断并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=6,BC=8,点O在对角线AC上,且OA=OB=OC,点P是边CD上的一个动点,连接OP,过点O作OQ⊥OP,交BC于点Q.
(1)求OB的长度;
(2)设DP= x,CQ= y,求y与x的函数表达式(不要求写自变量的取值范围);
(3)若
 OCQ是等腰三角形,求CQ的长度.
OCQ是等腰三角形,求CQ的长度.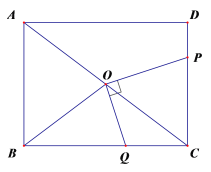
相关试题

