【题目】如图,![]() ABC中,∠ACB=90°,∠ABC=22.5°,将
ABC中,∠ACB=90°,∠ABC=22.5°,将![]() ABC 绕着点C顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,连接BE.下列说法中,正确的有( )
ABC 绕着点C顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,连接BE.下列说法中,正确的有( )
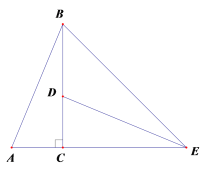
①DE⊥AB ②∠BCE是旋转角 ③∠BED=30° ④![]() BDE与
BDE与![]() CDE面积之比是
CDE面积之比是![]() :1
:1
A. 1个B. 2个C. 3个D. 4个
参考答案:
【答案】C
【解析】
延长ED交AB于点F,连接AD,根据直角三角形两锐角互余可得∠BAC=67.5°,根据旋转的性质可得∠BCE=∠ACD=90°,∠BCE是旋转角,CD=AC,CE=CB,∠CED=交ABC=22.5°,继而可得 ∠AFE=90°,即DE⊥AB,可得∠DAC=∠ADC=45°,∠CBE=∠CEB=45°,AD=![]() ,从而可得 ∠BAD=22.5°,∠BED=22.5°,从而可得 BD=AD=
,从而可得 ∠BAD=22.5°,∠BED=22.5°,从而可得 BD=AD=![]() CD,得到
CD,得到![]() BDE与
BDE与![]() CDE面积之比是
CDE面积之比是![]() :1,据此即可得出正确答案.
:1,据此即可得出正确答案.
延长ED交AB于点F,连接AD,
∵∠ACB=90°,∠ABC=22.5°,
∴∠BAC=90°-∠ABC=67.5°,
∵将![]() ABC 绕着点.顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,
ABC 绕着点.顺时针旋转,使得点A的对应点D落在边BC上,点B的对应点是点E,
∴∠BCE=∠ACD=90°,∠BCE是旋转角,CD=AC,CE=CB,∠CED=∠ABC=22.5°,
∴∠CED+∠BAC=90°,∴∠AFE=90°,即DE⊥AB,
∵∠BCE=∠ACD=90°,CD=AC,CE=CB,
∴∠DAC=∠ADC=45°,∠CBE=∠CEB=45°,AD=![]() ,
,
∴∠BAD=67.5°-45°=22.5°,∠BED=∠BEC-∠DEC=45°-22.5°=22.5°,
∴∠BAD=∠ABD,
∴BD=AD=![]() CD,
CD,
∴![]() BDE与
BDE与![]() CDE面积之比是BD:CD=
CDE面积之比是BD:CD=![]() :1,
:1,
综上可知,正确的是①②④,共3个,
故选C.

-
科目: 来源: 题型:
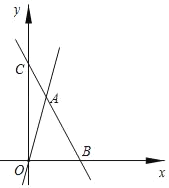
查看答案和解析>>【题目】已知:一个正比例函数与一个一次函数的图象交于点A(1,4)且一次函数的图象与x轴交于点B(3,0),坐标原点为O.
(1)求正比例函数与一次函数的解析式;
(2)若一次函数交与y轴于点C,求△ACO的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司在某市五个区投放共享单车供市民使用,投放量的分布及投放后的使用情况统计如下.
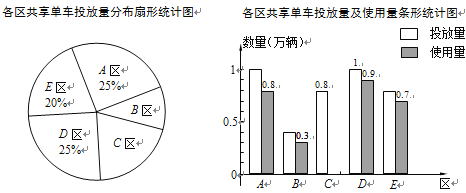
(1)该公司在全市一共投放了 万辆共享单车;
(2)在扇形统计图中,B区所对应扇形的圆心角为 °;
(3)该公司在全市投放的共享单车的使用量占投放量的85%,请计算C区共享单车的使用量并补全条形统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在直角坐标系中,A(﹣2,4)B(﹣4,2);A1、B1是A、B关于y轴的对称点;
(1)请在图中画出A、B关于原点O的对称点A2,B2(保留痕迹,不写作法);并直接写出A1、A2、B1、B2的坐标.
(2)试问:在x轴上是否存在一点C,使△A1B1C的周长最小,若存在求C点的坐标,若不存在说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 OAB是边长为4的等边三角形,OD是AB边上的高,点P是OD上的一个动点,若点C的坐标是
OAB是边长为4的等边三角形,OD是AB边上的高,点P是OD上的一个动点,若点C的坐标是 ,则PA+PC的最小值是_________________.
,则PA+PC的最小值是_________________.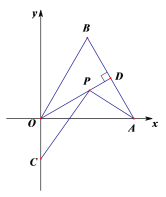
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,
 ABC的顶点均在格点上.
ABC的顶点均在格点上.(1)先将
 ABC向上平移4个单位后得到的
ABC向上平移4个单位后得到的 A1B1C1,再将
A1B1C1,再将 A1B1C1绕点C1按顺时针方向旋转90°后所得到的
A1B1C1绕点C1按顺时针方向旋转90°后所得到的 A2B2 C1,在图中画出
A2B2 C1,在图中画出 A1B1C1和
A1B1C1和 A2B2 C1.
A2B2 C1.(2)
 A2B2 C1能由
A2B2 C1能由 ABC绕着点O旋转得到,请在网格上标出点O.
ABC绕着点O旋转得到,请在网格上标出点O.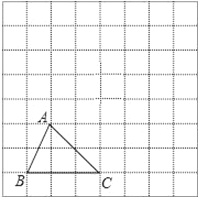
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
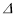 ABC中,∠A=80°,BD、CE分别平分∠ABC、∠ACB,BD与CE交于点F.
ABC中,∠A=80°,BD、CE分别平分∠ABC、∠ACB,BD与CE交于点F. (1)求∠BFC的度数;
(2)如图2,EG、DG分别平分∠AEF、∠ADF, EG与DG交于点G ,求∠EGD的度数.
相关试题

