【题目】如图所示,已知△ABC,分别以AB、AC边作图:AE⊥AB,AF⊥AC,AE=AB,AF=AC,下列结论①△AEC≌△ABF,②EC=FB,③EC⊥FB,④MA平分∠EMF中,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】∵AE⊥AB,AF⊥AC,
∴∠EAB=∠FAC=90°,
∴∠EAB+∠BAC=∠FAC+∠BAC,
∴∠EAC=∠BAF,
在△AEC和△ABF中
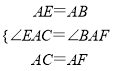
∴△AEC≌△ABF(SAS);
故①正确;
∵△AEC≌△ABF(已证)
∴EC=FB;
故②正确;
∵△AEC≌△ABF,
∴∠ACE=∠AFB,
∵∠FAC=90°,
∴∠AFB+∠AOF=90°,
∴∠ACE+∠AOF=90°,
∵∠AOF=∠COM,
∴∠ACE+∠COM=90°,
∴∠CMF=180°-90°=90°,
∴EC⊥BF;
故③正确;
作AP⊥CE于P,AQ⊥BF于Q,如图所示:
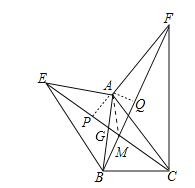
∵△EAC≌△BAF,
∴AP=AQ(全等三角形对应边上的高相等).
∵AP⊥CE于P,AQ⊥BF于Q,
∴AM平分∠EMF.
故④正确;
综合上述可得:①②③④共计4个正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
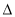 ABC的中线AD、BE相交于点F,下列结论正确的有 ( )
ABC的中线AD、BE相交于点F,下列结论正确的有 ( )①S△ABD=S△DCA;② S△AEF=S△BDF;③S四边形EFDC=2S△AEF;④S△ABC=3S△ABF
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.下列结论错误的是( )

A. ∠C=2∠A B. BD平分∠ABC C. S△BCD=S△BOD D. 点D为线段AC的黄金分割点
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费.甲厂的总费用y1(干元)、乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示.

(l)甲厂的制版费为____千元,印刷费为平均每个 元,甲厂的费用yl与证书数量x之间的函数关系式为 ,
(2)当印制证书数量不超过2千个时,乙厂的印刷费为平均每个 元;
(3)当印制证书数量超过2干个时,求乙厂的总费用y2与证书数量x之间的函数关系[式;
(4)若该单位需印制证书数量为8干个,该单位应选择哪个厂更节省费用?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=ax2+bx+5的图象过A(﹣1,0),B(5,0)两点,与y轴交于点C,作直线BC,动点P从点C出发,以每秒
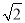 个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.(1)求抛物线的表达式;
(2)如图2,当t=1时,若点Q是X轴上的一个动点,如果以Q,P,B为顶点的三角形与△ABC相似,求出Q点的坐标;
(3)如图3,过点P向x轴作垂线分别交x轴,抛物线于E、F两点.
①求PF的长度关于t的函数表达式,并求出PF的长度的最大值;
②连接BF,将△PBF沿BF折叠得到△P′BF,当t为何值时,四边形PFP′B是菱形?
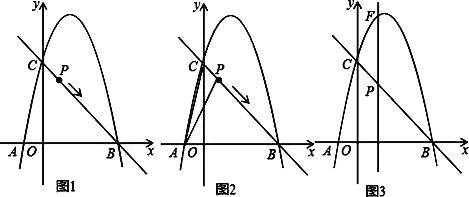
-
科目: 来源: 题型:
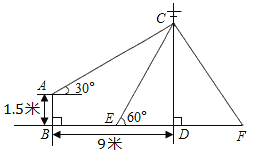
查看答案和解析>>【题目】如图,电力公司在电线杆上的C处引两条等长的拉线CE、CF固定电线杆CD,拉线CE和地面成60°角,在离电线杆9米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米.
(1)求CD的长(结果保留根号);
(2)求EF的长(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】2004年4月我国铁路第5次大提速。假设Kl20次空调快速列车的平均速度提速后比提速前提高了44千米/时,提速前的列车时刻表如下:
行驶区间
车次
起始时刻
到站时刻
历时
全程里程
A地—B地
K120
2:00
6:00
4小时
264千米
请你根据题目提供的信息,填写提速后的列车时刻表,并写出计算过程。
行驶区间
车次
起始时刻
到站时刻
历时
全程里程
A地—B地
K120
2:00
264千米
相关试题

