【题目】如图, ![]() ABC的中线AD、BE相交于点F,下列结论正确的有 ( )
ABC的中线AD、BE相交于点F,下列结论正确的有 ( )
①S△ABD=S△DCA;② S△AEF=S△BDF;③S四边形EFDC=2S△AEF;④S△ABC=3S△ABF
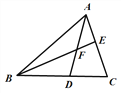
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】∵AD是△ABC的中线,
∴S△ABD=S△DCA=![]() ,故①正确;
,故①正确;
∵BE分别是是△ABC的中线,
∴S△ABE=S△BCE=![]() ,
,
∴S△ABD=S△DCA= S△ABE=S△BCE,
∴S△ABE=S△ABD,
∴S△ABE- S△ABF =S△ABD- S△ABF,
∴S△AEF=S△BDF,故②正确;
∵△ABC的中线AD、BE相交于点F,
∴S△ABF =2S△AEF.
∵S△DCA=S△ABE,
∴S△DCA- S△AEF =S△ABE- S△AEF,
∴S△ABF =S四边形EFDC,
∴S四边形EFDC=2S△AEF,故③正确;
∵△ABC的中线AD、BE相交于点F,
∴S△ABE=![]() .
.
∵S△ABC=2 S△ABE,
∴S△ABE=3 S△ABF,故④正确;
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=
 的图象的两个交点.
的图象的两个交点.(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)若D(x,0)是x轴上原点左侧的一点,且满足kx+b-
 <0,求x的取值范围.
<0,求x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】电脑中有一种游戏——蜘蛛纸牌,开始游戏前有500分的基本分,游戏规则如下:①操作一次减x分;②每完成一列加y分.有一次小明在玩这种“蜘蛛纸牌”游戏时,随手用表格记录了两个时段的电脑显示:
第一时段
第二时段
完成列数
2
5
分数
634
898
操作次数
66
102
(1)通过列方程组,求x,y的值;
(2)如果小明最终完成此游戏(即完成10列),分数是1 182,问他一共操作了多少次?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为
为 的直径,
的直径,  为弦
为弦 的中点,连接
的中点,连接 并延长交
并延长交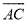 于点
于点 ,过点
,过点 作
作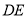 ∥
∥ ,交
,交 的延长线于点
的延长线于点 ,连接
,连接 ,
,  .
.
(1)求证:
 是⊙
是⊙ 的切线;
的切线;(2)若
 时,
时,①求图中阴影部分的面积;
②以
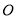 为原点,
为原点,  所在的直线为
所在的直线为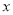 轴,直径
轴,直径 的垂直平分线为
的垂直平分线为 轴,建立如图所示的平面直角坐标系,试在线段
轴,建立如图所示的平面直角坐标系,试在线段 上求一点
上求一点 ,使得直线
,使得直线 把阴影部分的面积分成
把阴影部分的面积分成 的两部分.
的两部分. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.下列结论错误的是( )

A. ∠C=2∠A B. BD平分∠ABC C. S△BCD=S△BOD D. 点D为线段AC的黄金分割点
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费.甲厂的总费用y1(干元)、乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示.

(l)甲厂的制版费为____千元,印刷费为平均每个 元,甲厂的费用yl与证书数量x之间的函数关系式为 ,
(2)当印制证书数量不超过2千个时,乙厂的印刷费为平均每个 元;
(3)当印制证书数量超过2干个时,求乙厂的总费用y2与证书数量x之间的函数关系[式;
(4)若该单位需印制证书数量为8干个,该单位应选择哪个厂更节省费用?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC,分别以AB、AC边作图:AE⊥AB,AF⊥AC,AE=AB,AF=AC,下列结论①△AEC≌△ABF,②EC=FB,③EC⊥FB,④MA平分∠EMF中,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
相关试题

