【题目】如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.下列结论错误的是( )

A. ∠C=2∠A B. BD平分∠ABC C. S△BCD=S△BOD D. 点D为线段AC的黄金分割点
参考答案:
【答案】C
【解析】试题解析:A、∵∠A=36°,AB=AC,
∴∠C=∠ABC=72°,
∴∠C=2∠A,正确,
B、∵DO是AB垂直平分线,
∴AD=BD,
∴∠A=∠ABD=36°,
∴∠DBC=72°-36°=36°=∠ABD,
∴BD是∠ABC的角平分线,正确,
C,根据已知不能推出△BCD的面积和△BOD面积相等,错误,
D、∵∠C=∠C,∠DBC=∠A=36°,
∴△DBC∽△CAB,
∴![]() ,
,
∴BC2=CDAC,
∵∠C=72°,∠DBC=36°,
∴∠BDC=72°=∠C,
∴BC=BD,
∵AD=BD,
∴AD=BC,
∴AD2=CDAC,
即点D是AC的黄金分割点,正确,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】电脑中有一种游戏——蜘蛛纸牌,开始游戏前有500分的基本分,游戏规则如下:①操作一次减x分;②每完成一列加y分.有一次小明在玩这种“蜘蛛纸牌”游戏时,随手用表格记录了两个时段的电脑显示:
第一时段
第二时段
完成列数
2
5
分数
634
898
操作次数
66
102
(1)通过列方程组,求x,y的值;
(2)如果小明最终完成此游戏(即完成10列),分数是1 182,问他一共操作了多少次?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为
为 的直径,
的直径,  为弦
为弦 的中点,连接
的中点,连接 并延长交
并延长交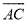 于点
于点 ,过点
,过点 作
作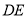 ∥
∥ ,交
,交 的延长线于点
的延长线于点 ,连接
,连接 ,
,  .
.
(1)求证:
 是⊙
是⊙ 的切线;
的切线;(2)若
 时,
时,①求图中阴影部分的面积;
②以
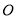 为原点,
为原点,  所在的直线为
所在的直线为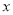 轴,直径
轴,直径 的垂直平分线为
的垂直平分线为 轴,建立如图所示的平面直角坐标系,试在线段
轴,建立如图所示的平面直角坐标系,试在线段 上求一点
上求一点 ,使得直线
,使得直线 把阴影部分的面积分成
把阴影部分的面积分成 的两部分.
的两部分. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
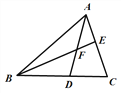
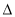 ABC的中线AD、BE相交于点F,下列结论正确的有 ( )
ABC的中线AD、BE相交于点F,下列结论正确的有 ( )①S△ABD=S△DCA;② S△AEF=S△BDF;③S四边形EFDC=2S△AEF;④S△ABC=3S△ABF
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费.甲厂的总费用y1(干元)、乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示.

(l)甲厂的制版费为____千元,印刷费为平均每个 元,甲厂的费用yl与证书数量x之间的函数关系式为 ,
(2)当印制证书数量不超过2千个时,乙厂的印刷费为平均每个 元;
(3)当印制证书数量超过2干个时,求乙厂的总费用y2与证书数量x之间的函数关系[式;
(4)若该单位需印制证书数量为8干个,该单位应选择哪个厂更节省费用?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC,分别以AB、AC边作图:AE⊥AB,AF⊥AC,AE=AB,AF=AC,下列结论①△AEC≌△ABF,②EC=FB,③EC⊥FB,④MA平分∠EMF中,正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
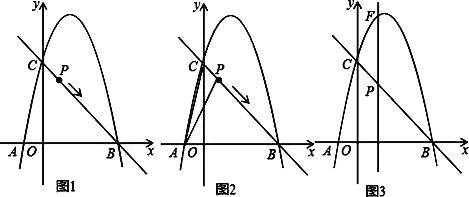
查看答案和解析>>【题目】如图1,抛物线y=ax2+bx+5的图象过A(﹣1,0),B(5,0)两点,与y轴交于点C,作直线BC,动点P从点C出发,以每秒
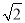 个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.(1)求抛物线的表达式;
(2)如图2,当t=1时,若点Q是X轴上的一个动点,如果以Q,P,B为顶点的三角形与△ABC相似,求出Q点的坐标;
(3)如图3,过点P向x轴作垂线分别交x轴,抛物线于E、F两点.
①求PF的长度关于t的函数表达式,并求出PF的长度的最大值;
②连接BF,将△PBF沿BF折叠得到△P′BF,当t为何值时,四边形PFP′B是菱形?
相关试题

