【题目】在直角坐标系xOy中,A(0,2)、B(﹣1,0),将△ABO经过旋转、平移变化后得到如图1所示的△BCD.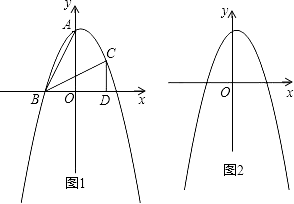
(1)求经过A、B、C三点的抛物线的解析式;
(2)连结AC,点P是位于线段BC上方的抛物线上一动点,若直线PC将△ABC的面积分成1:3两部分,求此时点P的坐标;
(3)现将△ABO、△BCD分别向下、向左以1:2的速度同时平移,求出在此运动过程中△ABO与△BCD重叠部分面积的最大值.
参考答案:
【答案】
(1)
解:∵A(0,2)、B(﹣1,0),将△ABO经过旋转、平移变化得到△BCD,
∴BD=OA=2,CD=OB=1,∠BDC=∠AOB=90°.
∴C(1,1).
设经过A、B、C三点的抛物线解析式为y=ax2+bx+c,
则有 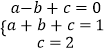 ,
,
∴ 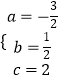
∴抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
解:如图1所示,
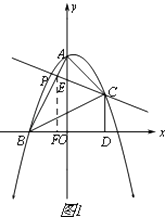
设直线PC与AB交于点E.
∵直线PC将△ABC的面积分成1:3两部分,
∴ ![]() =
= ![]() 或
或 ![]() =3,
=3,
过E作EF⊥OB于点F,则EF∥OA.
∴△BEF∽△BAO,
∴ ![]() .
.
∴当 ![]() =
= ![]() 时,
时, ![]() ,
,
∴EF= ![]() ,BF=
,BF= ![]() ,
,
∴E(﹣ ![]() ,
, ![]() )
)
∴直线PC解析式为y=﹣ ![]() x+
x+ ![]() ,
,
∴﹣ ![]() x2+
x2+ ![]() x+2=﹣
x+2=﹣ ![]() x+
x+ ![]() ,
,
∴x1=﹣ ![]() ,x2=1(舍去),
,x2=1(舍去),
∴P(﹣ ![]() ,
, ![]() ),
),
当 ![]() 时,同理可得,P(﹣
时,同理可得,P(﹣ ![]() ,
, ![]() )
)
(3)
解:设△ABO平移的距离为t,△A1B1O1与△B2C1D1重叠部分的面积为S.
(i) 当0<t< ![]() 时,△A1B1O1与△B2C1D1重叠部分为四边形.
时,△A1B1O1与△B2C1D1重叠部分为四边形.
由平移得,A1B1的解析式为y=2x+2﹣t,A1B1与x轴交点坐标为M( ![]() ,0).
,0).
C1B2的解析式为y= ![]() x+t+
x+t+ ![]() ,C1B2与y轴交点坐标为N(0,t+
,C1B2与y轴交点坐标为N(0,t+ ![]() ).
).
①如图2,当C1D1在y轴右侧时,即0<t≤ ![]() 时,重叠部分是现四边形ONQM,
时,重叠部分是现四边形ONQM,
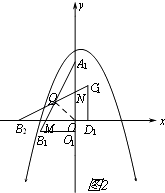
设A1B1与x轴交于点M,C1B2与y轴交于点N,A1B1与C1B2交于点Q,连结OQ.
由 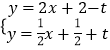 ,
,
∴ 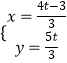 ,
,
∴Q( ![]() ,
, ![]() ).
).
∴S=S△QMO+S△QON
= ![]() ×
× ![]() ×
× ![]() +
+ ![]() ×(t+
×(t+ ![]() )×
)× ![]()
=﹣ ![]() t2+t+
t2+t+ ![]()
=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() .
.
∵0<t≤ ![]() ,
,
∴当t= ![]() 时,S的最大值为
时,S的最大值为 ![]() .
.
②如图4,当C'D'在y轴左侧,即: ![]() <t<
<t< ![]() 时,点C'在△A'MO内部,其重叠部分是四边形C'QMD',
时,点C'在△A'MO内部,其重叠部分是四边形C'QMD',
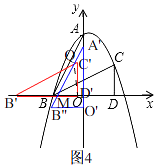
同(Ⅰ)的方法得出:Q( ![]() ,
, ![]() ).
).
∴S=S△QMD'+S△QON
= ![]() ×[
×[ ![]() ﹣(2t﹣1)]×
﹣(2t﹣1)]× ![]() +
+ ![]() ×1×[
×1×[ ![]() ﹣(2t﹣1)]
﹣(2t﹣1)]
=﹣ ![]() t2+1
t2+1
∵ ![]() <t<
<t< ![]() ,
,
∴S< ![]() <
< ![]()
(ii)如图3所示,

当 ![]() ≤t<
≤t< ![]() 时,△A1B1O1与△B2C1D1重叠部分为直角三角形.
时,△A1B1O1与△B2C1D1重叠部分为直角三角形.
设A1B1与x轴交于点H,A1B1与C1D1交于点G.
∴G(1﹣2t,4﹣5t),
∴D1H= ![]() +1﹣2t=
+1﹣2t= ![]() ,D1G=4﹣5t.
,D1G=4﹣5t.
∴S= ![]() D1H×D1G=
D1H×D1G= ![]() ×
× ![]() ×(4﹣5t)=
×(4﹣5t)= ![]() (5t﹣4)2.
(5t﹣4)2.
∴当 ![]() ≤t<
≤t< ![]() 时,S的最大值为
时,S的最大值为 ![]() .
.
综上所述,在此运动过程中△ABO与△BCD重叠部分面积的最大值为 ![]() .
.
【解析】(1)由旋转,平移得到C(1,1),用待定系数法求出抛物线解析式;(2)先判断出△BEF∽△BAO,再分两种情况进行计算,由面积比建立方程求解即可;(3)先由平移得到A1B1的解析式为y=2x+2﹣t,A1B1与x轴交点坐标为( ![]() ,0).C1B2的解析式为y=
,0).C1B2的解析式为y= ![]() x+t+
x+t+ ![]() ,C1B2与y轴交点坐标为(0,t+
,C1B2与y轴交点坐标为(0,t+ ![]() ),再分两种情况进行计算即可.
),再分两种情况进行计算即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作发现:

(1)数学活动课上,小明将已知△ABO(如图1)绕点O旋转180°得到△CDO(如图2).小明发现线段AB与CD有特殊的关系,请你写出:线段AB与CD的关系是 .
(2)连结AD(如图3),观察图形,试说明AB+AD>2AO.
(3)连结BC(如图4),观察图形,直接写出图中全等的三角形:
(写出三对即可) .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在反比例函数y=﹣
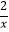 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= 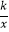 的图象上运动.若tan∠CAB=2,则k的值为( )
的图象上运动.若tan∠CAB=2,则k的值为( ) 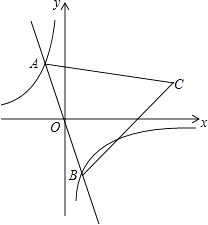
A.2
B.4
C.6
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2
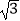 ,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将
,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将  绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为
绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为 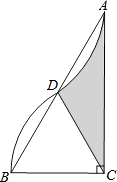
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中
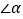 的变化情况,解答下列问题.
的变化情况,解答下列问题.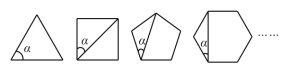
(1)将下面的表格补充完整:

(2)根据规律,是否存在一个正n边形,使其中的
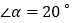 ?若存在,直接写出
?若存在,直接写出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(3)根据规律,是否存在一个正n边形,使其中的
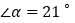 ?若存在,直接写出
?若存在,直接写出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y.

(1)当x为何值时,OP⊥AP?
(2)求y与x的函数关系式,并写出x的取值范围;
(3)在点P的运动过程中,是否存在x,使△OCM的面积与△ABP的面积之和等于△EMP的面积?若存在,请求x的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=
 ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.
相关试题

