【题目】操作发现:

(1)数学活动课上,小明将已知△ABO(如图1)绕点O旋转180°得到△CDO(如图2).小明发现线段AB与CD有特殊的关系,请你写出:线段AB与CD的关系是 .
(2)连结AD(如图3),观察图形,试说明AB+AD>2AO.
(3)连结BC(如图4),观察图形,直接写出图中全等的三角形:
(写出三对即可) .
参考答案:
【答案】(1)AB=CD,AB//CD;(2)证明见解析;(3)ΔABO![]() ΔCDO,ΔADO
ΔCDO,ΔADO![]() ΔCBO,ΔABC
ΔCBO,ΔABC![]() ΔCDA,ΔABD
ΔCDA,ΔABD![]() ΔCDB
ΔCDB
【解析】(1)根据图形旋转的性质即可得出结论;
(2)根据三角形三边不等关系得AD+CD>AC,再由旋转的性质得AC=2AO,从而得出结论;
(3)根据三角形全等的判定条件可得出结论.
(1)根据旋转的性质可得:ΔABO![]() ΔCDO,
ΔCDO,
∴AB=CD,∠ABO=∠CDO,
∴AB//CD,
故线段AB与CD的关系是:AB=CD,AB//CD;
(2)在ΔACD中,AD+CD>AC
又因为AB=CD,AO=OC
所以AB+AD>2AO
(3)ΔABO![]() ΔCDO,ΔADO
ΔCDO,ΔADO![]() ΔCBO,ΔABC
ΔCBO,ΔABC![]() ΔCDA,ΔABD
ΔCDA,ΔABD![]() ΔCDB.
ΔCDB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,E 是直线 CD 上的一点,且 ∠BAE=30°, 是直线 CD 上的一动点,M是 AP 的中点,直线 MN⊥AP 且与 CD 交于点 N,设 ∠BAP=X°,∠MNE=Y°.

(1)在图2 中,当 x=12 时,∠MNE= ;在图 3 中,当 x=50 时,∠MNE= ;

(2)研究表明:y与x之间关系的图象如图4所示( 不存在时,用空心点表示),请你根据图象直接估计当 y=100 时,x= ;

(3)探究:当 x= 时,点 N 与点 E 重合;
(4)探究:当 x>105 时,求y与x之间的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】云南地区地震发生后,市政府筹集了必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)

(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能求出这三种车型分别有多少辆吗?此时的运费又是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在反比例函数y=﹣
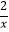 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第一象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= 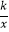 的图象上运动.若tan∠CAB=2,则k的值为( )
的图象上运动.若tan∠CAB=2,则k的值为( ) 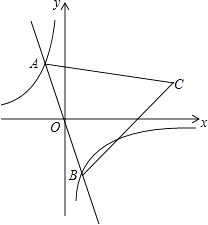
A.2
B.4
C.6
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2
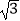 ,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将
,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将  绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为
绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为 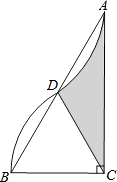
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,A(0,2)、B(﹣1,0),将△ABO经过旋转、平移变化后得到如图1所示的△BCD.
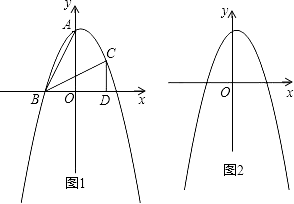
(1)求经过A、B、C三点的抛物线的解析式;
(2)连结AC,点P是位于线段BC上方的抛物线上一动点,若直线PC将△ABC的面积分成1:3两部分,求此时点P的坐标;
(3)现将△ABO、△BCD分别向下、向左以1:2的速度同时平移,求出在此运动过程中△ABO与△BCD重叠部分面积的最大值.
相关试题

