【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下。(单位:km)![]()
(1)求收工时距A地多远?
(2)在第______次纪录时距A地最远。
(3)若每千米耗油0.3升,问共耗油多少升?
参考答案:
【答案】五
【解析】(1)按照规定,将各数相加,由结果判断收工时距A地多远;(2)先由绝对值之和求出总路程,再算总的耗油量.
解:(1)根据题意列式-4+7-9+8+6-5-2=1km.
答:收工时距A地1km,在A的东面.
(2)由题意得,第一次距A地|-4|=4千米;第二次距A地-4+7=3千米;第三次距A地|-4+7-9|=6千米;第四次距A地|-4+7-9+8|=2千米;第五次距A地|-4+7-9+8+6|=8千米;第六次距A地|-4+7-9+8+6-5|=3千米;第五次距A地|-4+7-9+8+6-5-2|=1千米;所以在第五次纪录时距A地最远.
故答案为:五.
(3)根据题意得检修小组走的路程为:
|-4|+|+7|+|-9|+8|+|+6|+|-5|+|-2|=41(km)
41×0.3=12.3升.
答:检修小组工作一天需汽油12.3升.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个边长为
 的大正方形和两个边长为b的小正方形,分别将他们按照图①和图②的形式摆放,
的大正方形和两个边长为b的小正方形,分别将他们按照图①和图②的形式摆放,
(1)用含有
 的代数式分别表示阴影面积:
的代数式分别表示阴影面积: ,
, ,
, .
.(2)若
 ,求
,求 的值;
的值;(3)若
 ,
, ,
, ,求出图③中的阴影部分面积.
,求出图③中的阴影部分面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,
 D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且
D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且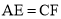 连接EF并取EF的中点O,连接DO并延长至点G,使
连接EF并取EF的中点O,连接DO并延长至点G,使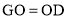 ,连接DE,DF,GE,GF
,连接DE,DF,GE,GF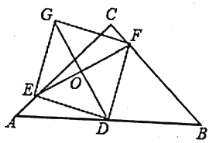
(1)求证:四边形EDFG是正方形;
(2)直接写出当点E在什么位置时,四边形EDFG的面积最小?最小值是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b分别交x轴、y轴于A(1,0)、B(0,﹣1),交双曲线y=
 于点C、D.
于点C、D.(1)求k、b的值;
(2)写出不等式kx+b>
 的解集.
的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“2018年某明星演唱会”于6月3日在某市奥体中心举办.小明去离家300的奥体中心看演唱会,到奥体中心后,发现演唱会门票忘带了,此时离演唱会开始还有30分钟,于是他跑步回家,拿到票后立刻找到一辆“共享单车”原路赶回奥体中心,已知小明骑车的时间比跑步的时间少用了5分钟,且骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小明跑步的平均速度;
(2)如果小明在家取票和寻找“共享单车”共用了4分钟,他能否在演唱会开始前赶到奥体中心?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方形ABCD中,点E、F、G分别是边AD、AB、BC的中点,连接EP、FG.
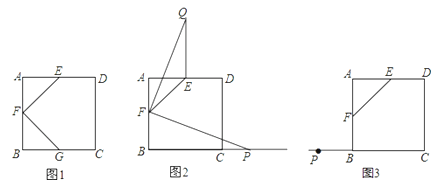
(1)如图1,直接写出EF与FG的关系____________;
(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转90°,得到线段FH,连接EH.
①求证:△FFE≌△PFG;②直接写出EF、EH、BP三者之间的关系;
(3)如图3,若点P为CB延长线上的一动点,连接FP,按照(2)中的做法,在图(3)中补全图形,并直接写出EF、EH、BP三者之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果点E、F、G、H分别是四边形ABCD四条边的中点,若EFGH为菱形,则四边形应具备的下列条件中,不正确的个数是( )
①一组对边平行而另一组对边不平行; ②对角线互相平分;③对角线互相垂直;④对角线相等
A. 1个B. 2个C. 3个D. 4个
相关试题

