【题目】如图,在等腰直角三角形ABC中,![]() D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且
D是AB的中点,E,F分别是AC,BC.上的点(点E不与端点A,C重合),且![]() 连接EF并取EF的中点O,连接DO并延长至点G,使
连接EF并取EF的中点O,连接DO并延长至点G,使![]() ,连接DE,DF,GE,GF
,连接DE,DF,GE,GF
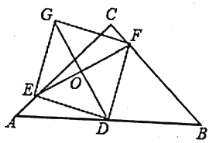
(1)求证:四边形EDFG是正方形;
(2)直接写出当点E在什么位置时,四边形EDFG的面积最小?最小值是多少?
参考答案:
【答案】(1)详见解析;(2)当点E为线段AC的中点时,四边形EDFG的面积最小,该最小值为4
【解析】
(1)连接CD,根据等腰直角三角形的性质可得出∠A=∠DCF=45°、AD=CD,结合AE=CF可证出△ADE≌△CDF(SAS),根据全等三角形的性质可得出DE=DF、ADE=∠CDF,通过角的计算可得出∠EDF=90°,再根据O为EF的中点、GO=OD,即可得出GD⊥EF,且GD=2OD=EF,由此即可证出四边形EDFG是正方形;
(2)过点D作DE′⊥AC于E′,根据等腰直角三角形的性质可得出DE′的长度,从而得出2≤DE<2![]() ,再根据正方形的面积公式即可得出四边形EDFG的面积的最小值.
,再根据正方形的面积公式即可得出四边形EDFG的面积的最小值.
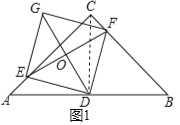
(1)证明:连接CD,如图1所示.
∵![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
D是AB的中点,
∴![]()
在![]() 和
和![]() 中
中![]() ,
,
∴ ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 为等腰直角三角形.
为等腰直角三角形.
∵O为EF的中点,![]() ,
,
∴![]() ,且
,且![]() ,
,
∴四边形EDFG是正方形;
(2)解:过点D作![]() 于E′,如图2所示.
于E′,如图2所示.

∵![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
∴![]() ,点E′为AC的中点,
,点E′为AC的中点,
∴![]() (点E与点E′重合时取等号).
(点E与点E′重合时取等号).
∴![]()
∴当点E为线段AC的中点时,四边形EDFG的面积最小,该最小值为4
-
科目: 来源: 题型:
查看答案和解析>>【题目】小强打算找印刷公司设计一款新年贺卡并印刷.如图1是甲印刷公司设计与印刷卡片计价方式的说明(包含设计费与印刷费),乙公司的收费与印刷卡片数量的关系如图2所示.
(1)分别写出甲乙两公司的收费y(元)与印刷数量x之间的关系式.
(2)如果你是小强,你会选择哪家公司?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】聪聪参加我市电视台组织的“阳光杯”智力竞答节目,答对最后两道单选题就顺利通关,第一道单选题有
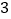 个选项,第二道单选题有4个选项,这两道题聪聪都不会,不过聪聪还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).
个选项,第二道单选题有4个选项,这两道题聪聪都不会,不过聪聪还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项).(1)如果聪聪两次“求助”都在第一道题中使用,那么聪聪通关的概率是 .
(2)如果聪聪将每道题各用一次“求助”,请用树状图或者列表来分析他顺利通关的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个边长为
 的大正方形和两个边长为b的小正方形,分别将他们按照图①和图②的形式摆放,
的大正方形和两个边长为b的小正方形,分别将他们按照图①和图②的形式摆放,
(1)用含有
 的代数式分别表示阴影面积:
的代数式分别表示阴影面积: ,
, ,
, .
.(2)若
 ,求
,求 的值;
的值;(3)若
 ,
, ,
, ,求出图③中的阴影部分面积.
,求出图③中的阴影部分面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b分别交x轴、y轴于A(1,0)、B(0,﹣1),交双曲线y=
 于点C、D.
于点C、D.(1)求k、b的值;
(2)写出不等式kx+b>
 的解集.
的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下。(单位:km)
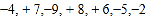
(1)求收工时距A地多远?
(2)在第______次纪录时距A地最远。
(3)若每千米耗油0.3升,问共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“2018年某明星演唱会”于6月3日在某市奥体中心举办.小明去离家300的奥体中心看演唱会,到奥体中心后,发现演唱会门票忘带了,此时离演唱会开始还有30分钟,于是他跑步回家,拿到票后立刻找到一辆“共享单车”原路赶回奥体中心,已知小明骑车的时间比跑步的时间少用了5分钟,且骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小明跑步的平均速度;
(2)如果小明在家取票和寻找“共享单车”共用了4分钟,他能否在演唱会开始前赶到奥体中心?说明理由.
相关试题

