【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+![]() ∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )
∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )

A. ①② B. ③④ C. ①②④ D. ①③④
参考答案:
【答案】C
【解析】因为∠BAC和∠ABC的平分线相交于点O,所以∠OBA=![]() ∠CBA, ∠OAB=
∠CBA, ∠OAB=![]() ∠CAB,所以∠AOB=
∠CAB,所以∠AOB=![]() ∠CBA-
∠CBA-![]() ∠CAB=
∠CAB=![]() =90°+
=90°+ ![]() , ①正确,
, ①正确,
因为EF∥AB,所以∠FOB=∠ABO,又∠ABO=∠FBO,所以∠FOB=∠FBO,所以FO=FB,
同理EO=EA,所以AE+BF=EF, ②正确,
当∠C=![]() 时,AE+BF=EF<CF+CE,所以E,F分别是AC,BC的中点, ③错误,
时,AE+BF=EF<CF+CE,所以E,F分别是AC,BC的中点, ③错误,
作OH⊥AC于H,
因为∠BAC和∠ABC的平分线相交于点O,所以点O在∠C的平分线上,
所以OD=OH,所以S△CEF= ![]() , ④正确,
, ④正确,
故选C.
-
科目: 来源: 题型:
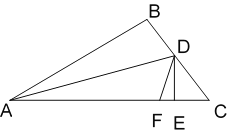
查看答案和解析>>【题目】已知,如图,在△ABC中,AD平分∠BAC,DE、DF分别是△ADC的高和角平分线(∠C >∠DAC).
(1)若∠B=80°,∠C=40°,求∠DAE的度数;
(2)试猜想∠EDF、∠C与∠DAC有何种关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a+a2=2a3B.a2a3=a6C.(a2)3=a5D.a6÷a3=a3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是
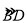 的中点,CE⊥AB于E,BD交CE于点F.
的中点,CE⊥AB于E,BD交CE于点F.(1)求证:CF﹦BF;
(2)若CD﹦6,AC﹦8,则⊙O的半径为 ,CE的长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0
(1)求证:方程有两个实数根;
(2)当k为何值时,此方程的两个实数根互为相反数;
(3)我们定义:若一元二次方程ax2+bx+c=0的两个正实数根x1、x2(x1>x2),满足2<
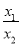 <3,则称这个一元二次方程有两个“梦想根”.如果关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个“梦想根”,求k的范围.
<3,则称这个一元二次方程有两个“梦想根”.如果关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个“梦想根”,求k的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在第1个△A1BC中,∠B=50°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是_____________.
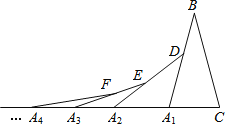
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答.

(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:图
a
b
c
d
顶点数(S)
7
边数(M)
9
区域数(N)
3
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有条边.
相关试题

