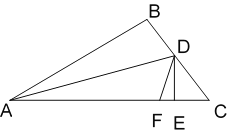
【题目】已知,如图,在△ABC中,AD平分∠BAC,DE、DF分别是△ADC的高和角平分线(∠C >∠DAC).
(1)若∠B=80°,∠C=40°,求∠DAE的度数;
(2)试猜想∠EDF、∠C与∠DAC有何种关系?并说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,理由见解析.
,理由见解析.
【解析】试题分析:(1)先利用三角形内角和定理计算出∠![]() ,然后利用角平分线的定义可得∠DAE=
,然后利用角平分线的定义可得∠DAE= ![]() ,(2)根据三角形内角和定理可得: ∠
,(2)根据三角形内角和定理可得: ∠![]() -∠DAC-∠C,利用角平分线的定义可得: ∠CDF=
-∠DAC-∠C,利用角平分线的定义可得: ∠CDF=![]() ∠
∠![]() =
=![]() (
(![]() -∠DAC-∠C)=90°-
-∠DAC-∠C)=90°-![]() (∠DAC+∠C),利用直角三角形两锐角互余可得: ∠CDE=90°-∠C,所以∠EDF=∠CDF-∠CDE=
(∠DAC+∠C),利用直角三角形两锐角互余可得: ∠CDE=90°-∠C,所以∠EDF=∠CDF-∠CDE=![]() (∠C-∠DAC).试题解析:(1)
(∠C-∠DAC).试题解析:(1)![]() 在
在 ![]() 中,
中, ![]() ,
,![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,
,
![]() ,
,
(2) ![]() 理由如下:
理由如下:
在![]() 中,
中,
![]() ,
, ![]() ,
,
![]() 平分
平分![]() ,
,![]() ,
,
![]() 是
是![]() 的高,
的高, ![]() ,
,
![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果+3吨表示运入仓库的大米吨数, 那么运出5吨大米表示为( )
A.-3吨
B.+3吨
C.-5吨
D.+5吨 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的“三阶等腰线”.
(1)请你在图1,图2中用两种不同的方法画出顶角为36°的等腰三角形的“三阶等腰线”,并标注每个等腰三角形顶角的度数.(若两种方法分得的三角形成3对全等三角形,则视为同一种).
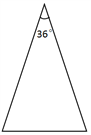



图1 图2 备用1 备用2
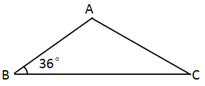
(2)△ABC中,∠B=36°,AD和DE是△ABC的“三阶等腰线”,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2﹣4x+k=0有两个不相等的实数根
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程x2﹣4x+k=0与x2+mx﹣1=0有一个相同的根,求此时m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a+a2=2a3B.a2a3=a6C.(a2)3=a5D.a6÷a3=a3
-
科目: 来源: 题型:
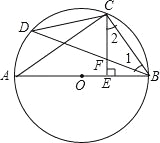
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是
 的中点,CE⊥AB于E,BD交CE于点F.
的中点,CE⊥AB于E,BD交CE于点F.(1)求证:CF﹦BF;
(2)若CD﹦6,AC﹦8,则⊙O的半径为 ,CE的长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+
 ∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )
∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )
A. ①② B. ③④ C. ①②④ D. ①③④
相关试题

