【题目】已知:关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0
(1)求证:方程有两个实数根;
(2)当k为何值时,此方程的两个实数根互为相反数;
(3)我们定义:若一元二次方程ax2+bx+c=0的两个正实数根x1、x2(x1>x2),满足2<![]() <3,则称这个一元二次方程有两个“梦想根”.如果关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个“梦想根”,求k的范围.
<3,则称这个一元二次方程有两个“梦想根”.如果关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个“梦想根”,求k的范围.
参考答案:
【答案】(1)证明见解析(2)1(3)﹣![]() <k<-
<k<-![]() 或﹣3<k<﹣2
或﹣3<k<﹣2
【解析】
试题分析:(1)根据方程的判别式,可得答案;
(2)根据互为相反数的和为零,可得关于k的方程,根据解方程,可得答案;
(3)根据方程的梦想根,可得不等式组,根据解不等式组,可得答案.
试题解析:(1)关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0,
a=k,b=﹣(k﹣1),c=﹣1,
△=b2﹣4ac=[﹣(k﹣1)]2﹣4k(﹣1)=k2+2k+1=(k+1)2≥0,
关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个实数根;
(2)关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0,
x1=![]() ,x2=
,x2=![]() ,
,
方程的两个实数根互为相反数,得
x1+x2=![]() +
+![]() =0,
=0,
即![]() =0,
=0,
解得k=1,
当k=1时,此方程的两个实数根互为相反数;
(3)当k>0时,x1=1,x2=﹣![]() <0,不符合题意;
<0,不符合题意;
当﹣1≤k<0时,x1=﹣![]() ,x2=1,2<
,x2=1,2<![]() <3,得
<3,得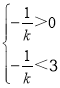 ,
,
解得﹣![]() <k<-
<k<-![]() ;
;
当k<﹣1时,x1=﹣![]() ,x2=1,由2<
,x2=1,由2<![]() <3,得2<﹣k<3,
<3,得2<﹣k<3,
解得﹣3<k<﹣2不符合题意舍去,
综上所述:于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个“梦想根”,k的范围是:
﹣![]() <k<-
<k<-![]() 或﹣3<k<﹣2.
或﹣3<k<﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a+a2=2a3B.a2a3=a6C.(a2)3=a5D.a6÷a3=a3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是
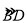 的中点,CE⊥AB于E,BD交CE于点F.
的中点,CE⊥AB于E,BD交CE于点F.(1)求证:CF﹦BF;
(2)若CD﹦6,AC﹦8,则⊙O的半径为 ,CE的长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+
 ∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )
∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )
A. ①② B. ③④ C. ①②④ D. ①③④
-
科目: 来源: 题型:
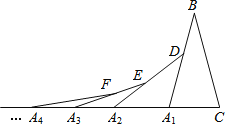
查看答案和解析>>【题目】如图,在第1个△A1BC中,∠B=50°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答.

(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:图
a
b
c
d
顶点数(S)
7
边数(M)
9
区域数(N)
3
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有条边. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的布袋中装有除颜色外其余都相同的红、黄、蓝球共200个,墨墨通过多次摸球试验后发现,其中摸到红色球和蓝色球的频率稳定在25%和55%,则口袋中可能有黄球个.
.
相关试题

