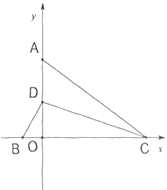
【题目】如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB,与y轴交于D点,∠CAO=90°-∠BDO.
(1)求证:AC=BC:
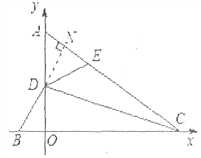
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;

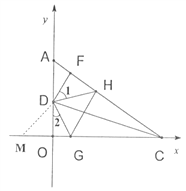
(3)如图3,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,当H在FC上移动、点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
 (图3)
(图3)
参考答案:
【答案】(1)证明见解析;(2)8;(3)GH=FH+OG,证明见解析.
【解析】试题分析: (1)由题意∠CAO=90°-∠BDO,可知∠CAO=∠CBD,CD平分∠ACB与y轴交于D点,所以可由AAS定理证明△ACD≌△BCD,由全等三角形的性质可得AC=BC;
(2)过D作DN⊥AC于N点,可证明Rt△BDO≌Rt△EDN、△DOC≌△DNC,因此,BO=EN、OC=NC,所以,BC+EC=BO+OC+NC-NE=2OC,即可得BC+EC的长;
(3)在x轴的负半轴上取OM=FH,可证明△DFH≌△DOM、△HDG≌△MDG,因此,MG=GH,所以,GH=OM+OG=FH+OG,即可证明所得结论.
试题解析:
(1)证明:∵∠CAO=90°-∠BDO,
∴∠CAO=∠CBD.
又∵∠ACD=∠BCD,CD=CD,
∴△ACD≌△BCD(AAS).
∴AC=BC.
(2)解:过D作DN⊥AC于N点,如图所示:
∵∠ACD=∠BCD,∠DOC=∠DNC=90°,
CD=CD
∴△DOC≌△DNC(AAS),
∴DO=DN,OC=NC.
又∵∠DEA=∠DBO,∠DOB=∠DNC=90°
∴△BDO≌△EDN(AAS),
∴BO=EN.
∴BC+EC=BO+OC+NC-NE=2OC=8.
(3)GH=FH+OG.
证明:由(1)知:DF=DO,
在x轴的负半轴上取OM=FH,连接DM,
如图所示:
在△DFH和△DOM中
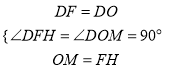
∴△DFH≌△DOM(SAS).
∴DH=DM,∠l=∠ODM.
∴∠GDH=∠1+∠2=∠ODM+∠2=∠GDM.
在△HDG和△MDG中
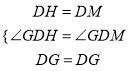
∴△HDG≌△MDG(SAS).
∴MG=GH,
∴GH=OM+OG=FH+OG.
点睛: 本题主要考查了全等三角形的判定及其性质,做题时添加了辅助线,正确作出辅助线是解决问题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三条边都相等的三角形叫做等边三角形,它的三个角都是60°. △ABC是等边三角形,点D在BC所在直线上运动,连接AD,在AD所在直线的右侧作∠DAE=60°,交△ABC的外角∠ACF的角平分线所在直线于点E.
(1)如图1,当点D在线段BC上时,请你猜想AD与AE的大小关系,并给出证明;
(2)如图2,当点D在线段BC的反向延长线上时,依据题意补全图形,请问上述结论还成立吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“ 六一”儿童节前夕,蕲黄县教育局准备给留守儿童赠送一批学习用品,先对浠泉镇浠泉小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6 名,7 名,8 名,10 名,12 名这五种情形,并将统计结果绘制成了如图所示的两幅不完整的统计图.

请根据上述统计图,解答下列问题:
(1)该校有多少个班级?并补全条形统计图;
(2)该校平均每班有多少名留守儿童?留守儿童人数的众数是多少?
(3)若该镇所有小学共有60 个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,并解答问题.
将分式
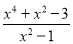 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式. 解:由分母为x2-1,可设x4+x2-3=(x2-1)(x2+a)+b.
则x4+x2-3=(x2-1)(x2+a)+b=x4-x2+ax2-a+b=x4+(a-1)x2-a+b
∴
 ,∴
,∴
∴

这样,分式
 被拆分成了一个整式x2+2与一个分式-
被拆分成了一个整式x2+2与一个分式- 的和.
的和. 根据上述作法,将分式
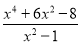 拆分成一个整式与一个分式(分子为整数)的和的形式。
拆分成一个整式与一个分式(分子为整数)的和的形式。 -
科目: 来源: 题型:
查看答案和解析>>【题目】若3m-12与12-3m都有平方根,则m的平方根为_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到△A1OB1,若点B的坐标为(2,1),则点B的对应点B1的坐标为( )
A. (1,2) B. (2,-1) C. (-2,1) D. (-2,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地是一个降水丰富的地区,今年4月初,由于连续降雨导致该地某水库水位持续上涨,经观测水库1日—4日的水位变化情况,发现有这样规律, 1日,水库水位为
 米,此后日期每增加一天,水库水位就上涨
米,此后日期每增加一天,水库水位就上涨 米。
米。(1)请求出该水库水位
 (米)与日期
(米)与日期 (日)之间的函数表达式;(注:4月1日,即
(日)之间的函数表达式;(注:4月1日,即 ,4月2日,即
,4月2日,即 ,…,以次类推)
,…,以次类推)(2)请用求出的函数表达式预测该水库今年4月6日的水位.
相关试题

