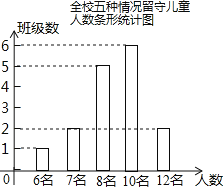
【题目】“ 六一”儿童节前夕,蕲黄县教育局准备给留守儿童赠送一批学习用品,先对浠泉镇浠泉小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6 名,7 名,8 名,10 名,12 名这五种情形,并将统计结果绘制成了如图所示的两幅不完整的统计图.

请根据上述统计图,解答下列问题:
(1)该校有多少个班级?并补全条形统计图;
(2)该校平均每班有多少名留守儿童?留守儿童人数的众数是多少?
(3)若该镇所有小学共有60 个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
参考答案:
【答案】(1)16,作图见试题解析;(2)9,10;(3)540.
【解析】试题分析:(1)根据有7名留守儿童班级有2个,所占的百分比是12.5%,即可求得班级的总个数;
(2)利用平均数的计算公式求得每班的留守儿童数,然后根据众数的定义,就是出现次数最多的数确定留守儿童的众数;
(3)利用班级数60乘以(2)中求得的平均数即可.
试题解析:(1)该校的班级数是:2÷12.5%=16(个).
则人数是8名的班级数是:16-1-2-6-2=5(个).
 ;
;
(2)每班的留守儿童的平均数是:![]() (1×6+2×7+5×8+6×10+12×2)=9(人),众数是10名;
(1×6+2×7+5×8+6×10+12×2)=9(人),众数是10名;
(3)该镇小学生中,共有留守儿童60×9=540(人).
答:该镇小学生中共有留守儿童540人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为( )
A. (1,2) B. (2,9) C. (5,3) D. (–9,–4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“泥兴陶,,是钦州的一张文化名片。钦州市某妮兴陶公司以每只60元的价格销售一种成本价为40元的文化纪念杯,每星期可售出100只。后来经过市场调查发现,每只杯子的售价每降低1元,则平均何星期可多买出10只。若该公司销售这种文化纪念杯要想平均每星期获利2240元,请回答:
(1)每只杯应降价多少元?
(2)在平均每星期获利不变的情况下,为尽可能让利于顾客,赢得市场,该公司应该按原售价的几折出售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】三条边都相等的三角形叫做等边三角形,它的三个角都是60°. △ABC是等边三角形,点D在BC所在直线上运动,连接AD,在AD所在直线的右侧作∠DAE=60°,交△ABC的外角∠ACF的角平分线所在直线于点E.
(1)如图1,当点D在线段BC上时,请你猜想AD与AE的大小关系,并给出证明;
(2)如图2,当点D在线段BC的反向延长线上时,依据题意补全图形,请问上述结论还成立吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料,并解答问题.
将分式
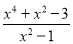 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式. 解:由分母为x2-1,可设x4+x2-3=(x2-1)(x2+a)+b.
则x4+x2-3=(x2-1)(x2+a)+b=x4-x2+ax2-a+b=x4+(a-1)x2-a+b
∴
 ,∴
,∴
∴

这样,分式
 被拆分成了一个整式x2+2与一个分式-
被拆分成了一个整式x2+2与一个分式- 的和.
的和. 根据上述作法,将分式
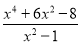 拆分成一个整式与一个分式(分子为整数)的和的形式。
拆分成一个整式与一个分式(分子为整数)的和的形式。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB,与y轴交于D点,∠CAO=90°-∠BDO.
(1)求证:AC=BC:
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;

(3)如图3,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,当H在FC上移动、点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
 (图3)
(图3) -
科目: 来源: 题型:
查看答案和解析>>【题目】若3m-12与12-3m都有平方根,则m的平方根为_________
相关试题

