【题目】某天放学后,小红步行,小丽骑自行车沿同一条笔直的马路到图书馆看书,图中线段OA、BC分别表示小红、小丽离开学校的路程s(米)与小红所用的时间t(分钟)的函数关系,根据图象解答下列问题:
(1)小丽比小红迟出发 分钟,小红步行的速度是 米/分钟;(直接写出结果)
(2)两人在路上相距不超过200米的时间有多少分钟?

参考答案:
【答案】(1)5,100;(2)4分钟
【解析】
(1)由点B的横坐标可得出小丽比小红迟出发5分钟;根据速度=路程÷时间,可求出小红步行的速度;
(2)根据点A、B、C的坐标,利用待定系数法可求出线段OA、BC的表达式,分相遇前及相遇后两种情况考虑,令两人之间的距离为200米,可求出两人正好相距200米的时间,二者做差即可求出结论.
解:(1)小丽比小红迟出发5分钟;
小红步行的速度为2000÷20=100(米/分钟).
故答案为:5;100;
(2)由图象知A(20,2000),B(5,0),C(15,2000),
设线段OA的函数表达式为s=kt(k≠0),
把A(20,2000)代入s=kt,得:2000=20k,
解得:k=100,
∴线段OA的函数表达式为s=100t(0≤t≤20);
设线段BC的函数表达式为s=mt+n(m≠0),
把B(5,0),C(15,2000)代入s=mt+n,得:
![]() ,解得:
,解得:![]() ,
,
∴线段BC的函数表达式为s=200t﹣1000(5≤t≤15),
若两人相遇前相距200米,则100t﹣(200t﹣1000)=200,
解得:t=8;
若两人相遇后相距200米,则(200t﹣1000)﹣100t=200,
解得:t=12,
∴12﹣8=4(分钟),
答:两人在路上相距不超过200米的时间有4分钟.
-
科目: 来源: 题型:
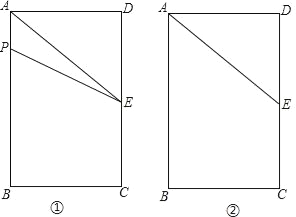
查看答案和解析>>【题目】如图①,长方形ABCD中,AB=6cm,BC=4cm,E为CD的中点.点P从A点出发,沿A﹣B﹣C的方向在长方形边上匀速运动,速度为1cm/s,运动到C点停止.设点P运动的时间为ts.(图②为备用图)
(1)当P在AB上,t= s时,△APE的面积为长方形面积的
 ;
;(2)整个运动过程中,t为何值时,△APE为直角三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=13,AC=20,BC=21,AD⊥BC,垂足为点D.
(1)求BD、CD的长;
(2)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一山顶有铁塔AB,从点P到铁塔底部B点有一条索道PB,索道长为300米,与水平线成角为α=30°,在P处测得A点的仰角为β=45°,试求铁塔的高AB.(精确到0.1米,其中
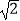 ≈1.41,
≈1.41,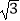 ≈1.73)
≈1.73)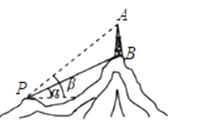
-
科目: 来源: 题型:
查看答案和解析>>【题目】在升旗结束后,小铭想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小铭从绳子末端C处拿起绳子后退至E点,求旗杆AB的高度和小铭后退的距离.(单位:米,参考数据:
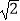 ≈1.41,
≈1.41,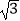 ≈1.73,结果保留一位小数)
≈1.73,结果保留一位小数)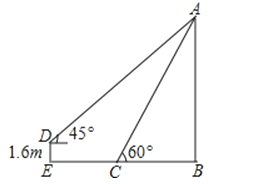
-
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A、B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和1台B种设备需要2.5万元.
(1)求每台A种、B种设备各多少万元?
(2)根据学校实际,需购进A种和B种设备共30台,总费用不超过30万元,请你通过计算,求至少购买A种设备多少台?
相关试题

