【题目】已知:如图,在△ABC中,AB=13,AC=20,BC=21,AD⊥BC,垂足为点D.
(1)求BD、CD的长;
(2)求△ABC的面积.

参考答案:
【答案】(1)BD=5,CD=16;(2)126
【解析】
(1)设BD=x,则CD=21﹣x.在Rt△ABD中,由勾股定理,得AD2=132﹣x2.在Rt△ACD中,由勾股定理,得AD2=202﹣(21﹣x)2.依此列出方程求出x,进一步得到CD的长;
(2)在Rt△ABD中,由勾股定理,得AD的长,再根据三角形面积公式即可求解.
解:(1)设BD=x,则CD=21﹣x,
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD中,由勾股定理,得AD2=AB2﹣BD2,
∴AD2=132﹣x2,
在Rt△ACD中,由勾股定理,得AD2=AC2﹣CD2,
∴AD2=202﹣(21﹣x)2,
∴132﹣x2=202﹣(21﹣x)2,
解得x=5,即BD=5,
∴CD=21﹣x=21﹣5=16;
(2)在Rt△ABD中,
由勾股定理,得AD=![]() =12,
=12,
∴S△ABC=![]() BCAD=
BCAD=![]() ×21×12=126.
×21×12=126.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条高速公路在城市A的东偏北30°方向直线延伸,县城M在城市A东偏北60°方向上,测验员从A沿高速公路前行4000米到达C,测得县城M位于C的北偏西60°方向上,现要设计一条从县城M进入高速公路的路线,请在高速公路上寻找连接点N,使修建到县城M的道路最短,试确定N点的位置并求出最短路线长.(结果取整数,
 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
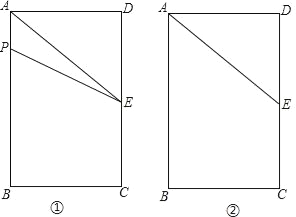
查看答案和解析>>【题目】如图①,长方形ABCD中,AB=6cm,BC=4cm,E为CD的中点.点P从A点出发,沿A﹣B﹣C的方向在长方形边上匀速运动,速度为1cm/s,运动到C点停止.设点P运动的时间为ts.(图②为备用图)
(1)当P在AB上,t= s时,△APE的面积为长方形面积的
 ;
;(2)整个运动过程中,t为何值时,△APE为直角三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天放学后,小红步行,小丽骑自行车沿同一条笔直的马路到图书馆看书,图中线段OA、BC分别表示小红、小丽离开学校的路程s(米)与小红所用的时间t(分钟)的函数关系,根据图象解答下列问题:
(1)小丽比小红迟出发 分钟,小红步行的速度是 米/分钟;(直接写出结果)
(2)两人在路上相距不超过200米的时间有多少分钟?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一山顶有铁塔AB,从点P到铁塔底部B点有一条索道PB,索道长为300米,与水平线成角为α=30°,在P处测得A点的仰角为β=45°,试求铁塔的高AB.(精确到0.1米,其中
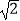 ≈1.41,
≈1.41,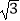 ≈1.73)
≈1.73)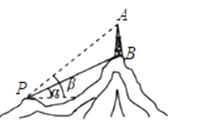
-
科目: 来源: 题型:
查看答案和解析>>【题目】在升旗结束后,小铭想利用所学数学知识测量学校旗杆高度,如图,旗杆的顶端垂下一绳子,将绳子拉直钉在地上,末端恰好至C处且与地面成60°角,小铭从绳子末端C处拿起绳子后退至E点,求旗杆AB的高度和小铭后退的距离.(单位:米,参考数据:
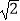 ≈1.41,
≈1.41,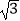 ≈1.73,结果保留一位小数)
≈1.73,结果保留一位小数)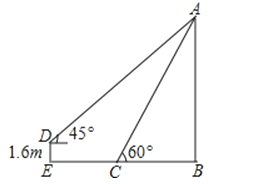
相关试题

