【题目】某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8:00~12:00,下午14:00~18:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于45件.
生产产品件数与所用时间之间的关系见下表:
生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(分) |
10 | 10 | 500 |
15 | 20 | 900 |
信息三:按件计酬,每生产一件甲产品可得6元,每生产一件乙产品可得10元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?
(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?
参考答案:
【答案】(1) 20,30;(2) 小王该月最多能得3970元,此时生产甲种产品45件,上产乙种产品370件.
【解析】
(1)设生产一件甲种产品需x分,生产一件乙种产品需y分,根据表中数据得出方程组,求出方程组的解即可;
(2)设生产甲种产品用x分,则生产乙种产品用(25×8×60-x)分,则生产甲种产品
![]() 件,生产乙种产品
件,生产乙种产品
![]() 件,根据题意得出W总额=6×
件,根据题意得出W总额=6×![]() +10×
+10×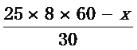 ,即可求出答案.
,即可求出答案.
1)设生产一件甲种产品需x分,生产一件乙种产品需y分,由题意得:![]()
即解这个方程组得:x=20,y=30,
即生产一件甲产品需要20分,生产一件乙产品需要30分;
(2)设生产甲种产品用x分,则生产乙种产品用(25×8×60-x)分,则生产甲种产品![]() 件,生产乙种产品
件,生产乙种产品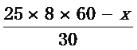 件,
件,
所以W总额=6×![]() +10×
+10×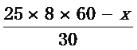 ,
,
=-![]() x+4000,
x+4000,
∵![]() ≥45,∴x≥900,
≥45,∴x≥900,
由一次函数的增减性,当,x=900时,W取得最大值,此时W=-![]() ×900+4000=3970(元),
×900+4000=3970(元),
此时甲有![]() =45(件),乙有:
=45(件),乙有: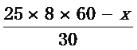 =370(件),
=370(件),
所以小王该月最多能得3970元,此时生产甲种产品45件,上产乙种产品370件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把方程(x-
 )(x+
)(x+  )+(2x-1)2=0化为一元二次方程的一般形式是( )
)+(2x-1)2=0化为一元二次方程的一般形式是( )
A.
B.
C.
D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程3x2-4x=2的根是( )
A.x1=-2,x2=1
B.x1= ,x2=
,x2= 
C.x1= ,x2=
,x2= 
D.x1= ,x2=
,x2= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程:2x2=5x+3的根是( )
A.x1=-6,x2=1
B.x1=3,x2=-1
C.x1=1,x2=
D.x1= - ,x2=3
,x2=3 -
科目: 来源: 题型:
查看答案和解析>>【题目】解一元二次方程x2-2x-5=0,结果正确的是( )
A.x1=-1+ ,x2=-1-
,x2=-1- 
B.x1=1+ ,x2=1-
,x2=1- 
C.x1=7,x2= 5
D.x1= 1+ ,x2=1-
,x2=1- 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知b2-4ac是一元二次方程ax2+bx+c=0(a≠0)的一个实数根,则ab的取值范围为( )
A.ab≥
B.ab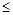

C.ab≥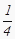
D.ab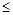
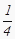
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2-x-3=0的较小根为x1 , 则下面对x1的估计正确的是( )
A.-2< x1<-1
B.-3< x1<-2
C.2< x1<3
D.-1< x1<0
相关试题

