【题目】已知b2-4ac是一元二次方程ax2+bx+c=0(a≠0)的一个实数根,则ab的取值范围为( )
A.ab≥ ![]()
B.ab ![]()
![]()
C.ab≥ ![]()
D.ab ![]()
![]()
参考答案:
【答案】B
【解析】解答:因为方程有实数解,故b2-4ac≥0.由题意有: ![]() =b2-4ac或
=b2-4ac或 ![]() =b2-4ac , 设u=
=b2-4ac , 设u= ![]() ,
,
则有2au2-u+b=0或2au2+u+b=0,(a≠0)
因为以上关于u的两个一元二次方程有实数解,
所以两个方程的判别式都大于或等于0,即得到1-8ab≥0,
所以ab≤ ![]() .
.
故选B.
分析:设u= ![]() ,利用求根公式得到关于u的两个一元二次方程,并且这两个方程都有实根,所以由判别式大于或等于0即可得到ab≤
,利用求根公式得到关于u的两个一元二次方程,并且这两个方程都有实根,所以由判别式大于或等于0即可得到ab≤ ![]()
【考点精析】关于本题考查的公式法,需要了解要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程:2x2=5x+3的根是( )
A.x1=-6,x2=1
B.x1=3,x2=-1
C.x1=1,x2=
D.x1= - ,x2=3
,x2=3 -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8:00~12:00,下午14:00~18:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于45件.
生产产品件数与所用时间之间的关系见下表:
生产甲产品件数(件)
生产乙产品件数(件)
所用总时间(分)
10
10
500
15
20
900
信息三:按件计酬,每生产一件甲产品可得6元,每生产一件乙产品可得10元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?
(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】解一元二次方程x2-2x-5=0,结果正确的是( )
A.x1=-1+ ,x2=-1-
,x2=-1- 
B.x1=1+ ,x2=1-
,x2=1- 
C.x1=7,x2= 5
D.x1= 1+ ,x2=1-
,x2=1- 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2-x-3=0的较小根为x1 , 则下面对x1的估计正确的是( )
A.-2< x1<-1
B.-3< x1<-2
C.2< x1<3
D.-1< x1<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )
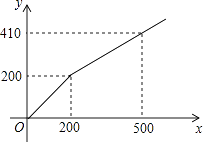
A.打八折
B.打七折
C.打六折
D.打五折 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

相关试题

