【题目】如图①,四边形ABCD中,BC∥AD,∠A=90°,点P从A点出发,沿折线AB→BC→CD运动,到点D时停止,已知△PAD的面积s与点P运动的路程x的函数图象如图②所示,则点P从开始到停止运动的总路程为( )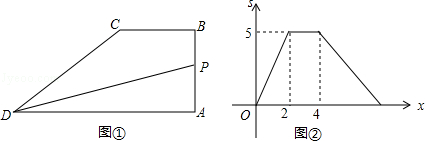
A.4
B.2+ ![]()
C.5
D.4+ ![]()
参考答案:
【答案】D
【解析】解:作CE⊥AD于点E,如下图所示,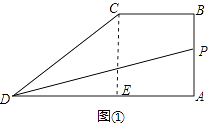
由图象可知,点P从A到B运动的路程是2,当点P与点B重合时,△ADP的面积是5,由B到C运动的路程为2,
∴ ![]() ,
,
解得,AD=5,
又∵BC∥AD,∠A=90°,CE⊥AD,
∴∠B=90°,∠CEA=90°,
∴四边形ABCE是矩形,
∴AE=BC=2,
∴DE=AD﹣AE=5﹣2=3,
∴CD= ![]() ,
,
∴点P从开始到停止运动的总路程为:AB+BC+CD=2+2+ ![]() =4+
=4+ ![]() ,
,
故选D.
根据函数图象可以直接得到AB、BC和三角形ADB的面积,从而可以求得AD的长,作辅助线AE⊥AD,从而可得CD的长,进而求得点P从开始到停止运动的总路程,本题得以解决.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小亮从家步行到公交车站台,乘公交车去学校. 图中的折线表示小亮的离家距离s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是

A. 他离家8km共用了30min B. 公交车的速度是350m/min
C. 他步行的速度是100m/min D. 他等公交车时间为6min
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD∥GE,AQ 平分∠FAC,交 BD 于 Q,∠GFA=50°,∠Q=25°,则∠ACB 的 度数( )
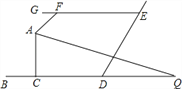
A. 90° B. 95° C. 100° D. 105°
-
科目: 来源: 题型:
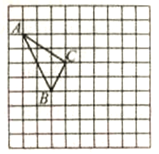
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为A(-4,5),C(-1,3).
(1)请在网格平面内作出平面直角坐标系(不写作法);
(2)请作出△ABC关于y轴对称△A'B'C';
(3)分别写出A'、B'、C'的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
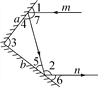
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2=________,∠3=________;
(2)在(1)中,若∠1=55°,则∠3=________;若∠1=40°,则∠3=________;
(3)由(1)、(2)请你猜想:当两平面镜a,b的夹角∠3=________时,可以使任何射到平面镜a上的光线m,经过平面镜a,b的两次反射后,入射光线m与反射光线n平行,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2 , 以OA2为直角边作等腰Rt△OA2A3 , …则OA6的长度为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b=0;②a+c>b;③抛物线y=ax2+bx+c与x轴的另一个交点为(3,0);④abc>0.其中正确的结论是(填写序号)

相关试题

