【题目】先阅读一段文字,再回答下列问题:
已知在平面内两点坐标P1(x1,y1),P2(x2,y2),其两点间距离公式为 ![]() ,同时,当两点所在的直线在坐标轴上或平行于x轴或垂直于x轴距离公式可简化成|x2-x1|或|y2-y1|.
,同时,当两点所在的直线在坐标轴上或平行于x轴或垂直于x轴距离公式可简化成|x2-x1|或|y2-y1|.
(1)已知A(3,5),B(-2,-1),试求A,B两点的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,试求A,B两点的距离.
(3)已知一个三角形各顶点坐标为A(0,6),B(-3,2),C(3,2),你能断定此三角形的形状吗?说明理由。
参考答案:
【答案】(1)![]() ;(2)6;(3)△ABC为等腰三角形,理由见解析
;(2)6;(3)△ABC为等腰三角形,理由见解析
【解析】
(1)根据点A、B的坐标利用两点间的距离公式即可求出A,B两点间的距离;
(2)设点A的坐标为(m,5),则点B的坐标为(m,-1),根据点A、B的坐标利用两点间的距离公式即可求出A,B两点间的距离;
(3)根据点A、B、C三点的坐标,利用两点间的距离公式即可求出线段AB、AC、BC的长度,由AB=AC即可得知△ABC为等腰三角形.
(1)∵A(3,5)、B(-2,-1),
∴AB=![]() .
.
故答案为:![]() .
.
(2)设点A的坐标为(m,5),则点B的坐标为(m,-1),
∴AB=![]() =6.
=6.
故答案为:6.
(3)△ABC为等腰三角形,理由如下:
∵A(0,6),B(-3,2),C(3,2),
∴AB=![]()
∴AB=AC,
∴△ABC为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A1B1C1;
(3)写出点B1的坐标;
(4)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC上的高,tanB=cos∠DAC.
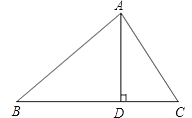
(1)求证:AC=BD;
(2)若sin∠C=
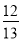 ,BC=12,求AD的长.
,BC=12,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们有时会碰上形如
 ,
, ,
, 的式子,其实我们可以将其进一步分母有理化.
的式子,其实我们可以将其进一步分母有理化.形如
 的式子还可以用以下方法化简:
的式子还可以用以下方法化简: .(*)
.(*)(1)请用不同的方法化简(写出化简过程):
(i)参照分母有理化的方法得
 ______________________________;
______________________________;(ii)参照(*)式的化简方法得
 ______________________________.
______________________________.(2)化简:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC中,点D、E、F分别在三边上,E是AC的中点,AD、BE、CF交于一点G,BD=2DC,S△GEC=3,S△GDC=4,则△ABC的面积是( )

A.25B..30C.35D.40
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ACB,BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC.以下结论:①AD∥BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠A+2∠BEC=180°;⑤DB平分∠ADC.其中正确的结论有( )

A.2个B.3个C.4个D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.

相关试题

