搜索
【题目】如图，在△ABC中，AD是BC上的高，tanB=cos∠DAC．
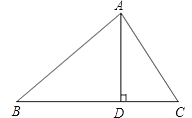
（1）求证：AC=BD；
（2）若sin∠C=
，BC=12，求AD的长．
参考答案：
【答案】（1）证明见解析（2）8
【解析】试题分析：（1）由于tanB=cos∠DAC，所以根据正切和余弦的概念证明AC=BD；
（2）设AD=12k，AC=13k，然后利用题目已知条件解直角三角形即可．
试题解析：解：（1）∵AD是BC上的高，∴AD⊥BC，∴∠ADB=90°，∠ADC=90°．在Rt△ABD和Rt△ADC中，∵tanB=
，cos∠DAC=
，tanB=cos∠DAC，∴
=
，∴AC=BD．
（2）在Rt△ADC中，sinC=
，故可设AD=12k，AC=13k，∴CD=
=5k，∵BC=BD+CD，AC=BD，∴BC=13k+5k=18k．由已知BC=12，∴18k=12，∴k=
，∴AD=12k=12×
=8．
-
科目： 来源： 题型：
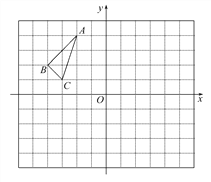
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)将△ABC向右平移2个单位长度,作出平移后的△A1B1C1,并写出△A1B1C1各顶点的坐标.
(2)若将△ABC绕点(-1,0)顺时针旋转180°后得到△A2B2C2,并写出△A2B2C2各顶点的坐标.
(3)观察△A1B1C1和△A2B2C2,它们是否关于某点成中心对称?若是,请写出对称中心的坐标;若不是,说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数分别填入相应的集合内：
，
，
，
，
，
，
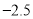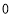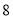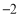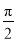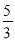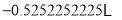（每两个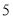 
之间依次增加 
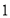个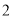 
）．（1）正数集合：{ ┄}；
（2）负数集合：{ ┄}；
（3）整数集合：{ ┄}；
（4）无理数集合：{ ┄}．
-
科目： 来源： 题型：
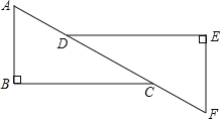
查看答案和解析>>【题目】 如图，两块形状、大小完全相同的三角板按照如图所示的样子放置，找一找图中是否有互相平行的线段，完成下面证明：
证明：
∵∠______=∠______，
∴______∥______（______）（填推理的依据）
-
科目： 来源： 题型：
查看答案和解析>>【题目】 某校七年级共有男生63名，为了参加全校运动会，七年级准备从本年级所有男生中挑选出身高相差不多的40名男生组成仪仗队，为此，收集到所有男生的身高数据（单位：cm），经过整理获得如下信息：
a．小明把所有男生的身高数据按由低到高整理为如下，但因为不小心有部分数据被墨迹遮挡：
b．小刚绘制了七年级所有男生身高的频数分布表
身高分组
划记
频数
149≤x＜152
丅
2
152≤x＜155
正一
6
155≤x＜158
正正丅
12
158≤x＜161
正正正
19
161≤x＜164
正正
10
164≤x＜167
______
______
167≤x＜170
______
______
170≤x＜173
丅
2
c．该校七年级男生身高的平均数、中位数、众数如下：
平均数
中位数
众数
160
m
n
根据以上信息，回答下列问题：
（1）补全b表中频数分布表；
（2）直接写出c表中m，n的值；
（3）借助于已给信息，确定挑选出参加仪仗队的男生的身高范围；
（4）若本区七年级共有男生1260名，利用以上数据估计，全区七年级男生身高达到160及以上的男生约有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：是长方形纸片ABCD折叠的情况，纸片的宽度AB=8cm，长AD=10cm，AD沿点A对折，点D正好落在BC上的M处，AE是折痕．
（1）求CM的长；
（2）求梯形ABCE的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】 如果一个正整数能表示为两个连续奇数的平方差，那么我们称这个正整数为“和谐数”，如8=32-12，16=52-32，24=72-52，因此，8，16，24这三个数都是“和谐数”．
（1）在32，75，80这三个数中，是和谐数的是______；
（2）若200为和谐数，即200可以写成两个连续奇数的平方差，则这两个连续奇数的和为______；
（3）小鑫通过观察发现以上求出的“和谐数”均为8的倍数，设两个连续奇数为2n-1和2n+1（其中n取正整数），请你通过运算验证“和谐数是8的倍数”这个结论是否正确．
相关试题
