【题目】如图,抛物线y=x2+bx+c(b、c为常数)与x轴相交于点A(﹣1,0)、B(3,0),与y轴相交于点C,其对称轴与x轴相交于点D,作直线BC.
(1)求抛物线的解析式.
(2)设点P为抛物线对称轴上的一个动点.
①如图①,若点P为抛物线的顶点,求△PBC的面积.
②是否存在点P使△PBC的面积为6?若存在,求出点P坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵抛物线y=x2+bx+c(b、c为常数)与x轴相交于点A(﹣1,0)、B(3,0),
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=x2﹣2x﹣3
(2)
解:①∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴P(1,4),且C(0,﹣3),
设直线BC解析式为y=kx+m,则有 ![]() ,解得
,解得 ![]() ,
,
∴直线BC解析式为y=x﹣3,
设对称轴交BC于点E,如图1,

则E(1,﹣2),
∴PE=﹣2﹣(﹣4)=2,
∴S△PBC= ![]() PEOB=
PEOB= ![]() ×3×2=3;
×3×2=3;
②设P(1,t),由①可知E(1,﹣2),
∴PE=|t+2|,
∴S△PBC= ![]() OBPE=
OBPE= ![]() |t+2|,
|t+2|,
∴ ![]() |t+2|=6,解得t=2或t=﹣6,
|t+2|=6,解得t=2或t=﹣6,
∴P点坐标为(1,2)或(1,﹣6),
即存在满足条件的点P,其坐标为(1,2)或(1,﹣6)
【解析】(1)把A、B两点坐标代入抛物线解析式,可求得b、c的值,可求得抛物线解析式;(2)①由抛物线解析式可求得P、C的坐标,可求得直线BC解析式,设对称轴交直线BC于点E,则可求得E点坐标,可求得PE的长,则可求得△PBC的面积;②设P(1,t),则可用t表示出△PBC的面积,可得到t的方程,则可求得P点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从邵阳市到长沙的高铁列车里程比普快列车里程缩短了75千米,运行时间减少了4小时,已知邵阳市到长沙的普快列车里程为306千米,高铁列车平均时速是普快列车平均时速的3.5倍.
(1)求高铁列车的平均时速;
(2)某日刘老师从邵阳火车南站到长沙市新大新宾馆参加上午11:00召开的会议,如果他买到当日上午9:20从邵阳市火车站到长沙火车南站的高铁票,而且从长沙火车南站到新大新宾馆最多需要20分钟.试问在高铁列车准点到达的情况下他能在开会之前赶到吗? -
科目: 来源: 题型:
查看答案和解析>>【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,
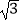 ≈1.73,精确到个位)
≈1.73,精确到个位) 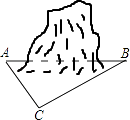
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)操作发现:如图,小明在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.
(2)问题解决:保持(1)中条件不变,若DC=2FC,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在Rt△ABC中,∠C=90°,sinA=
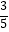 ,则tanB的值为( )
,则tanB的值为( )
A.
B.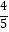
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作第1个正方形A1B1C1C;延长C1B1交x轴于点A2 , 作第2个正方形A2B2C2C1 , …,按这样的规律进行下去,第2016个正方形的面积是
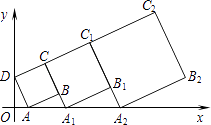
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,E是AC上一点,且AE=AB,∠EBC=
 ∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F.
∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F. 
(1)求证:BC与⊙O相切;
(2)若AB=8,sin∠EBC= ,求AC的长.
,求AC的长.
相关试题

