【题目】已知在Rt△ABC中,∠C=90°,sinA= ![]() ,则tanB的值为( )
,则tanB的值为( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】解:解法1:利用三角函数的定义及勾股定理求解. ∵在Rt△ABC中,∠C=90°,
∴sinA= ![]() ,tanB=
,tanB= ![]() 和a2+b2=c2 .
和a2+b2=c2 .
∵sinA= ![]() ,设a=3x,则c=5x,结合a2+b2=c2得b=4x.
,设a=3x,则c=5x,结合a2+b2=c2得b=4x.
∴tanB= ![]() .
.
故选A.
解法2:利用同角、互为余角的三角函数关系式求解.
∵A、B互为余角,
∴cosB=sin(90°﹣B)=sinA= ![]() .
.
又∵sin2B+cos2B=1,
∴sinB= ![]() =
= ![]() ,
,
∴tanB= ![]() =
= ![]() =
= ![]() .
.
故选A.
【考点精析】解答此题的关键在于理解锐角三角函数的定义的相关知识,掌握锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数,以及对互余两角的三角函数关系的理解,了解互余关系:sinA=cos(90°—A),cosA=sin(90°—A),tanA=cot(90°—A),cotA=tan(90°—A).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,
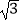 ≈1.73,精确到个位)
≈1.73,精确到个位) 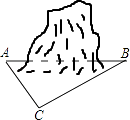
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)操作发现:如图,小明在矩形纸片ABCD的边AD上取中点E,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.
(2)问题解决:保持(1)中条件不变,若DC=2FC,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c(b、c为常数)与x轴相交于点A(﹣1,0)、B(3,0),与y轴相交于点C,其对称轴与x轴相交于点D,作直线BC.

(1)求抛物线的解析式.
(2)设点P为抛物线对称轴上的一个动点.
①如图①,若点P为抛物线的顶点,求△PBC的面积.
②是否存在点P使△PBC的面积为6?若存在,求出点P坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作第1个正方形A1B1C1C;延长C1B1交x轴于点A2 , 作第2个正方形A2B2C2C1 , …,按这样的规律进行下去,第2016个正方形的面积是
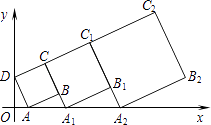
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,E是AC上一点,且AE=AB,∠EBC=
 ∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F.
∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F. 
(1)求证:BC与⊙O相切;
(2)若AB=8,sin∠EBC= ,求AC的长.
,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
 sin60°﹣4cos230°+sin45°tan60°+(
sin60°﹣4cos230°+sin45°tan60°+(  )﹣2 .
)﹣2 .
相关试题

