【题目】如图，抛物线y=﹣x2+bx+c与x轴交于A（1，0），B（﹣4，0）两点，

（1）求该抛物线的解析式；
（2）设（1）中的抛物线交y轴于C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由；
（3）设此抛物线与直线y=﹣x在第二象限交于点D，平行于y轴的直线 与抛物线交于点M，与直线y=﹣x交于点N，连接BM、CM、NC、NB，是否存在m的值，使四边形BNCM的面积S最大？若存在，请求出m的值，若不存在，请说明理由．

参考答案：

【答案】
（1）

解：∵抛物线y=﹣x2+bx+c与x轴交于A（1，0），B（﹣4，0）两点，

将A、B两点坐标代入抛物线方程，得到：

解得：

所以，该抛物线的解析式为：y=﹣x2﹣3x+4


（2）

解：存在．

∵由前面的计算可以得到，C（0，4），且抛物线的对称轴为直线x=﹣1.5，

∴由抛物线的对称性，点A、B关于直线x=1对称，

∴当QC+QA最小时，△QAC的周长就最小，

而当点Q在直线BC上时QC+QA最小，

此时直线BC的解析式为y=x+4，

当x=﹣1.5时，y=2.5，

∴在该抛物线的对称轴上存在点Q（﹣1.5，2.5），使得△QAC的周长最小


（3）

解：由题意，M（m，﹣m2﹣3m+4），N（m，﹣m）

∴线段MN=﹣m2﹣3m+4﹣（﹣m）=﹣m2﹣2m+4=﹣（m+1）2+5

∵S四边形BNCM=S△BMN+S△CMN=0.5MN×BO=2MN=﹣2（m+1）2+10

∴当m=﹣1时（在 内），四边形BNCM的面积S最大．


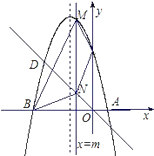
【解析】（1）A，B的坐标代入抛物线y=﹣x2+bx+c确定解析式．（2）A，B关于对称轴对称，BC与对称轴的交点就是点Q．（3）四边形BNCM的面积等于△MNB面积+△MNC的面积．
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点，以及对二次函数的性质的理解，了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．

关闭