【题目】高致病性禽流感是比SARS传染速度更快的传染病.为防止禽流感蔓延,政府规定:离疫点3km范围内为扑杀区;离疫点3km~5km范围内为免疫区,对扑杀区与免疫区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如图,在扑杀区内公路CD长为4km.
(1)请用直尺和圆规找出疫点O(不写作法,保留作图痕迹);
(2)求这条公路在免疫区内有多少千米?
参考答案:
【答案】
(1)
解: 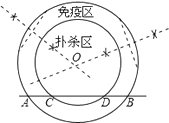
(2)
解:如图
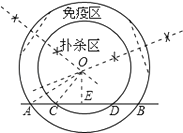
连接OA、OC,过点O作OE⊥AB于点E,
∴CE= ![]() CD=2km,AE=
CD=2km,AE= ![]() AB,
AB,
在Rt△OCE中,OE= ![]() =
= ![]() =
= ![]() km,
km,
在Rt△OAE中,AE= ![]() =
= ![]() =2
=2 ![]() km,
km,
∴AB=2AE=4 ![]() km,
km,
因此AC+BD=AB﹣CD=4 ![]() ﹣4(km).
﹣4(km).
答:这条公路在免疫区内有(4 ![]() ﹣4)千米
﹣4)千米
【解析】(1)在内圆(或外圆)任意作出两条弦,分别作出者两条弦的垂直平分线,它们的交点就是疫点(即圆心O);(2)利用垂径定理求出AB、CD的长度,问题解决.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为半圆直径,O为圆心,C为半圆上一点,E是弧AC的中点,OE交弦AC于点D,若AC=8cm,DE=2cm,求OD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的外角∠ACD的平分线CP与∠ABC平分线BP交于点P,若∠BPC=40°,则∠CAP的度数是( )
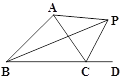
A. 30°; B. 40°; C. 50°; D. 60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】杨辉三角是一个由数字排列成等腰三角形数表,一般形式如图所示,其中每一横行都表示
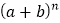 (此处
(此处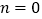 ,
, ,
, ,
, ,
, ,
,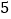 ,
, )的展开式中的系数,杨辉三角最本质的特征是,它的两条斜边都是由数字
)的展开式中的系数,杨辉三角最本质的特征是,它的两条斜边都是由数字 组成的,而其余的数则是等于它“肩”上的两个数之和.
组成的,而其余的数则是等于它“肩”上的两个数之和.















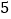

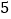








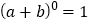






上图的构成规律你看懂了吗?
(1)请你直接写出
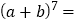 __________________.
__________________.杨辉三角还有另一个特征
(2)从第二行到第五行,每一行数字组成的数(如第三行为
 )都是上一行的数与_____积.
)都是上一行的数与_____积.(3)由此你可写出
 =_________________.
=_________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12cm,宽OB为4cm,隧道顶端D到路面的距离为10cm,建立如图所示的直角坐标系

(1)求该抛物线的解析式.
(2)一辆货运汽车载一长方体集装箱,集装箱最高处与地面距离为6m,宽为4m,隧道内设双向行车道,问这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面高度相等,如果灯离地面的高度不超过8.5m,那么两排灯的水平距离最小是多少米? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式的乘法中,能用平方差公式计算的是( )
A. (-m +n)(m - n) B. (
 a +b)(b -
a +b)(b - a)
a)C. (x + 5)(x + 5) D. (3a -4b)(3b +4a)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣4,0)两点,

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)设此抛物线与直线y=﹣x在第二象限交于点D,平行于y轴的直线 与抛物线交于点M,与直线y=﹣x交于点N,连接BM、CM、NC、NB,是否存在m的值,使四边形BNCM的面积S最大?若存在,请求出m的值,若不存在,请说明理由.
与抛物线交于点M,与直线y=﹣x交于点N,连接BM、CM、NC、NB,是否存在m的值,使四边形BNCM的面积S最大?若存在,请求出m的值,若不存在,请说明理由.
相关试题

