搜索
【题目】如图，长方体的长为
，宽为
，高为
，点
离点
的距离为
，一只蚂蚁如果要沿着长方体的表面从点
爬到点，需要爬行的最短距离是（ ）
A.
B.
C.
D.
参考答案：
【答案】B
【解析】
将长方体侧表面剪开与前面、上面、后面侧面分别形成一个长方形，分别利用勾股定理计算出AB的距离即可解答.
只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形，如图1：
因为长方体的宽为10，高为20，点B离点C的距离为5，
所以BD=CD+BC=10+5=15，AD=20
在直角三角形ABD中，根据勾股定理得：
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形，如图2：
此时BD=CD+BC=20+5=25,所以
同理与后面侧面所在构成一个长方形，如图3，
可求
因为
所以选B.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料：若m2﹣2mn+2n2﹣8n+16=0，求m、n的值．
解：∵m2﹣2mn+2n2﹣8n+16=0，∴（m﹣n）2=0，（n﹣4）2=0
∴（m2﹣2mn+n2）+（n2﹣8n+16）=0∴n=4，m=4．
∴（m﹣n）2+（n﹣4）2=0，
根据你的观察，探究下面的问题：
（1）已知x2﹣2xy+2y2+6y+9=0，求xy的值；
（2）已知△ABC的三边长a、b、c都是正整数，且满足a2+b2﹣10a﹣12b+61=0，求△ABC的最大边c的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点O是等边△ABC内一点．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．已知∠AOB=110°．
（1）求证：△COD是等边三角形；
（2）当α=150°时，试判断△AOD的形状，并说明理由；
（3）探究：当α为多少度时，△AOD是等腰三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】由于某地供水管爆裂.该地供水部门组织工人进行抢修.供水部门距离抢修工地15千米.抢修车装载着所需材料先从供水部门出发，15分钟后，工人乘吉普车从同一地点出发，结果他们同时到达抢修工地．已知吉普车速度是抢修车速度的1.5倍，求这两种车的速度.
-
科目： 来源： 题型：
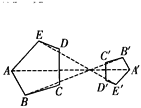
查看答案和解析>>【题目】如图，五边形ABCDE与五边形A'B'C'D'E'是位似图形，且位似比为2．如果五边形ABCDE的面积为16 cm2，周长为20 cm，那么五边形A'B'C'D'E'的面积为_______，周长为_______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某市积极开展“阳光体育进校园”活动，各校学生坚持每天锻炼一小时，某校根据实际，决定主要开设A：乒乓球，B：篮球，C：跑步，D：跳绳四种运动项目，为了解学生最喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图．请你结合图中信息解答下列问题．
（1）请计算最喜欢B项目的人数所占的百分比．
（2）请计算D项所在扇形图中的圆心角的度数．
（3）请把统计图补充完整．
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究：如图①，在△ABC 中，∠BAC＝90°，AB＝AC，直线 m 经过点 A，BD⊥m 于点 D，CE⊥m 于点 E，求证：△ABD≌△CAE．
应用：如图②，在△ABC 中，AB＝AC，D、A、E 三点都在直线 m 上，并且有∠BDA＝∠AEC＝∠BAC，求证：DE＝BD+CE．
相关试题
