【题目】如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.

(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
参考答案:
【答案】(1)证明见解析;(2)△AOD是直角三角形;(3)当α的度数为125 °或110 °或140 °时,△AOD是等腰三角形;
【解析】
(1)首先由旋转的定义和性质得到CO=CD,∠OCD=60°,然后根据等边三角形的判定方法即可得到△COD是等边三角形;(2)根据旋转前后对应的两个三角形全等可得△BOC≌△ADC,利用全等三角形的性质得到∠ADC=∠BOC=α=150°,再利用△COD是等边三角形得∠ODC=60°,于是可计算出∠ADO的度数,据此判断△AOD的形状;(3)需要分三种情况讨论,即①要使AO=AD,需∠AOD=∠ADO;②要使OA=OD,需∠OAD=∠ADO;③要使OD=AD,需∠OAD=∠AOD,再分别建立关于α的方程,求出α的度数;
解:
(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴CO=CD,∠OCD=60°,
∴△COD是等边三角形;
(2)当∠α=150°时,△AOD是直角三角形.理由如下:
∵将△BOC绕点C按顺时针方向旋转60°得△ADC,
∴△BOC≌△ADC,
∴∠ADC=∠BOC=150°,
又∵△COD是等边三角形,
∴∠ODC=60°,
∴∠ADO=∠ADC-∠ODC=90°,
∴△AOD是直角三角形;
(3)①要使AO=AD,需∠AOD=∠ADO,
∵∠AOD=360°-110°-60°-α=190°-α,∠ADO=α-60°,
∴190°-α=α-60°,
∴α=125°;
②要使OA=OD,需∠OAD=∠ADO,
∵∠OAD=180°-(∠AOD+∠ADO)=180°-(190°-α+α-60°)=50°,
∴α-60°=50°,
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD,
∵∠AOD=190°-α,∠OAD=![]() =120°-
=120°-![]() ,
,
∴190°-α=120°-![]() ,
,
解得α=140°.
综上所述:当α的度数为125 °或110 °或140 °时,△AOD是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC是等边三角形,D点是AC的中点,延长BC到E,使CE=CD.

(1)用尺规作图的方法,过D点作DM⊥BE,垂足是M(不写作法,保留作图痕迹);
(2)求证:BM=EM.
-
科目: 来源: 题型:
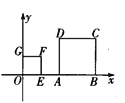
查看答案和解析>>【题目】如图,正方形OEFG和正方形ABCD是位似图形,点F的坐标为(1,1),点C的坐标为(4,2),则这两个正方形位似中心的坐标是______
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0,∴(m﹣n)2=0,(n﹣4)2=0
∴(m2﹣2mn+n2)+(n2﹣8n+16)=0∴n=4,m=4.
∴(m﹣n)2+(n﹣4)2=0,
根据你的观察,探究下面的问题:
(1)已知x2﹣2xy+2y2+6y+9=0,求xy的值;
(2)已知△ABC的三边长a、b、c都是正整数,且满足a2+b2﹣10a﹣12b+61=0,求△ABC的最大边c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于某地供水管爆裂.该地供水部门组织工人进行抢修.供水部门距离抢修工地15千米.抢修车装载着所需材料先从供水部门出发,15分钟后,工人乘吉普车从同一地点出发,结果他们同时到达抢修工地.已知吉普车速度是抢修车速度的1.5倍,求这两种车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体的长为
 ,宽为
,宽为 ,高为
,高为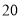 ,点
,点 离点
离点 的距离为
的距离为 ,一只蚂蚁如果要沿着长方体的表面从点
,一只蚂蚁如果要沿着长方体的表面从点 爬到点
爬到点 ,需要爬行的最短距离是( )
,需要爬行的最短距离是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
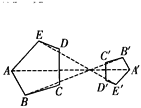
查看答案和解析>>【题目】如图,五边形ABCDE与五边形A'B'C'D'E'是位似图形,且位似比为2.如果五边形ABCDE的面积为16 cm2,周长为20 cm,那么五边形A'B'C'D'E'的面积为_______,周长为_______.
相关试题

