【题目】如图所示,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D.
(1)若BC=10,BD=6,则点D到AB的距离是多少?
(2)若∠BAD=30°,求∠B的度数.

参考答案:
【答案】(1)4.(2)30°.
【解析】
过点D作DE⊥AB于E,先求出CD,再根据角平分线上的点到角的两边的距离相等可得DE=CD,从而得解;
根据角平分线的定义可求出∠CAB的度数,再根据三角形内角和定理即可解答.
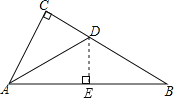
解: 1)过点D作DE⊥AB于E,
∵BC=8,BD=5,
∴CD=BC-BD=10-6=4,
∵∠C=90°,AD平分∠BAC,
∴DE=CD=4,
即点D到AB的距离是4;
(2) 因为AD平分∠BAC,
所以∠BAC=2∠BAD=60°.
又因为∠C=90°,
所以∠B=90°-60°=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=
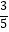 .
. 
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD 中,点P在对角线AC上,过P作EF∥AB,HG∥AD,记四边形BFPH的面积为S1,四边形DEPG的面积为S2,则S1与S2的大小关系是( )
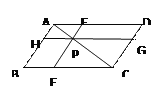
A. S1>S2 B. S1=S2 C. S1<S2 D. 无法判断
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰上的高与另一腰的夹角为360,则该等腰三角形的底角的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB,AC的垂直平分线分别交BC于D,E两点,垂足分别是M,N.
(1)若△ADE的周长是10,求BC的长;
(2)若∠BAC=100°,求∠DAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下表: 我们把某格中字母和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题:
序号
1
2
3
…
图形
x x
y
x xx x x
y y
x x x
y y
x x xx x x x
y y y
x x x x
y y y
x x x x
y y y
x x x x…
(1)第3格的“特征多项式”为 , 第4格的“特征多项式”为 , 第n格的“特征多项式”为;
(2)若第1格的“特征多项式”的值为﹣10,第2格的“特征多项式”的值为﹣16. ①求x,y的值;
②在①的条件下,第n格的“特征多项式”是否有最小值?若有,求出最小值和相应的n值;若没有,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
相关试题

