【题目】如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC= ![]() .
. 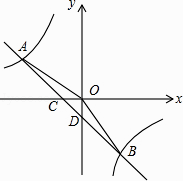
(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积.
参考答案:
【答案】
(1)解:过点A作AE⊥x轴于点E,如图所示.
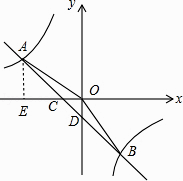
设反比例函数解析式为y= ![]() .
.
∵AE⊥x轴,
∴∠AEO=90°.
在Rt△AEO中,AO=5,sin∠AOC= ![]() ,∠AEO=90°,
,∠AEO=90°,
∴AE=AOsin∠AOC=3,OE= ![]() =4,
=4,
∴点A的坐标为(﹣4,3).
∵点A(﹣4,3)在反比例函数y= ![]() 的图象上,
的图象上,
∴3= ![]() ,解得:k=﹣12.
,解得:k=﹣12.
∴反比例函数解析式为y=﹣ ![]()
(2)解:∵点B(m,﹣4)在反比例函数y=﹣ ![]() 的图象上,
的图象上,
∴﹣4=﹣ ![]() ,解得:m=3,
,解得:m=3,
∴点B的坐标为(3,﹣4).
设直线AB的解析式为y=ax+b,
将点A(﹣4,3)、点B(3,﹣4)代入y=ax+b中得:
![]() ,解得:
,解得: ![]() ,
,
∴一次函数解析式为y=﹣x﹣1.
令一次函数y=﹣x﹣1中y=0,则0=﹣x﹣1,
解得:x=﹣1,即点C的坐标为(﹣1,0).
S△AOB= ![]() OC(yA﹣yB)=
OC(yA﹣yB)= ![]() ×1×[3﹣(﹣4)]=
×1×[3﹣(﹣4)]= ![]()
【解析】(1)过点A作AE⊥x轴于点E,设反比例函数解析式为y= ![]() .通过解直角三角形求出线段AE、OE的长度,即求出点A的坐标,再由点A的坐标利用待定系数法求出反比例函数解析式即可;(2)由点B在反比例函数图象上可求出点B的坐标,设直线AB的解析式为y=ax+b,由点A、B的坐标利用待定系数法求出直线AB的解析式,令该解析式中y=0即可求出点C的坐标,再利用三角形的面积公式即可得出结论.
.通过解直角三角形求出线段AE、OE的长度,即求出点A的坐标,再由点A的坐标利用待定系数法求出反比例函数解析式即可;(2)由点B在反比例函数图象上可求出点B的坐标,设直线AB的解析式为y=ax+b,由点A、B的坐标利用待定系数法求出直线AB的解析式,令该解析式中y=0即可求出点C的坐标,再利用三角形的面积公式即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校的复印任务原来由甲复印社承包,其收费y(元)与复印页数x(页)的关系如下表:
x(页)
100
200
400
1000
…
y(元)
40
80
160
400
…
(1)根据表格信息写出y与x之间的关系式;
(2)现在乙复印社表示:若学校每月先付200元的承包费,则可按每页0.15元收费.乙复印社每月收费y(元)与复印页数x(页)之间的关系式为_______________;
(3)若学校每月复印页数在1200页左右,应选择哪个复印社?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学骑自行车去郊外春游,骑行1小时后,自行车出现故障,维修好后继续骑行,下图表示他离家的距离y(千米)与所用的时间x(时)之间关系的图象.
(1)根据图象回答:小明到达离家最远的地方用了多长时间?此时离家多远?
(2)求小明出发2.5小时后离家多远;
(3)求小明出发多长时间离家12千米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了节约用水,采用分段收费标准.若某户居民每月应交水费y(元)与用水量x(吨)之间关系的图象如图,根据图象回答:
(1)该市自来水收费时,若使用不足5吨,则每吨收费多少元?超过5吨部分每吨收费多少元?
(2)若某户居民每月用水3.5吨,应交水费多少元?若某月交水费17元,该户居民用水多少吨?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD 中,点P在对角线AC上,过P作EF∥AB,HG∥AD,记四边形BFPH的面积为S1,四边形DEPG的面积为S2,则S1与S2的大小关系是( )
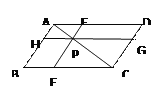
A. S1>S2 B. S1=S2 C. S1<S2 D. 无法判断
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形一腰上的高与另一腰的夹角为360,则该等腰三角形的底角的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D.
(1)若BC=10,BD=6,则点D到AB的距离是多少?
(2)若∠BAD=30°,求∠B的度数.

相关试题

