【题目】如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )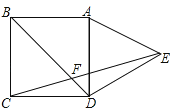
A.75°
B.70°
C.65°
D.60°
参考答案:
【答案】D
【解析】解:∵四边形ABCD是正方形,
∴∠ADC=90°,AD=DC,
又∵△ADE是正三角形,
∴CD=DE,∠ADE=60°,
∴△CDE是等腰三角形,∠CDE=90°+60°=150°,
∴∠ECD=∠DEC=15°,
∵∠BDC=45°,
∴∠CFD=180°﹣15°﹣45°=120°,
∴∠BFC=60°,
故选D
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数的平方根有_________,它们的和为___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在四边形ABCD中,BA=BC,∠ABC=60°,∠ADC=30°,连接对角线BD.
(1)将线段CD绕点C顺时针旋转60°得到线段CE,连接AE.
①依题意补全图1;
②试判断AE与BD的数量关系,并证明你的结论;
(2)在(1)的条件下,直接写出线段DA、DB和DC之间的数量关系;
(3)如图2,F是对角线BD上一点,且满足∠AFC=150°,连接FA和FC,探究线段FA、FB和FC之间的数量关系,并证明.
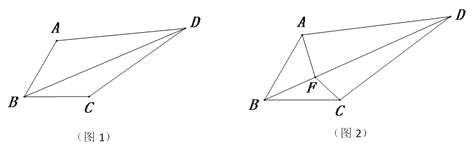
-
科目: 来源: 题型:
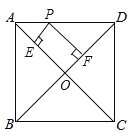
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=4,P是线段AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.2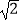
B.4
C.4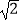
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】点P(m+3,m-2)在直角坐标系的x轴上,则点P的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的顶点坐标为(1,2),且经过点(3,10)求这条抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面文字,然后按要求解题.
例:1+2+3+…+100=?如果一个一个顺次相加显然太麻烦,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算,提高计算速度的.因为1+100=2+99=3+98=…=50+51=101,所以将所给算式中各加数经过交换、结合以后,可以很快求出结果:
1+2+3+4+5+…+100
=(1+100)+(2+99)+(3+98)+…+(50+51)
=101× = .
(1)补全例题解题过程;
(2)请猜想:1+2+3+4+5+6+…+(2n﹣2)+(2n﹣1)+2n= .
(3)试计算:a+(a+b)+(a+2b)+(a+3b)+…+(a+99b).
相关试题

