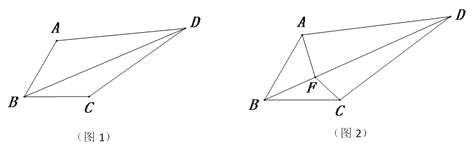
【题目】如图1,在四边形ABCD中,BA=BC,∠ABC=60°,∠ADC=30°,连接对角线BD.
(1)将线段CD绕点C顺时针旋转60°得到线段CE,连接AE.
①依题意补全图1;
②试判断AE与BD的数量关系,并证明你的结论;
(2)在(1)的条件下,直接写出线段DA、DB和DC之间的数量关系;
(3)如图2,F是对角线BD上一点,且满足∠AFC=150°,连接FA和FC,探究线段FA、FB和FC之间的数量关系,并证明.
参考答案:
【答案】(1)①图形见解析②AE=BD(2)判断: ![]() (3)判断
(3)判断![]() ,证明见解析
,证明见解析
【解析】试题分析:(1)①根据题意画图即可;
②连接AC,证明△BCD≌△ACE即可;
(2)连接DE,可证三角形ADE为直角三角形,由勾股定理即可得出结论;
(3)将线段CF绕点C顺时针旋转60°得到线段CE,连接EF、EA,证明△BCD≌△ACE和直角三角形AEF,结合勾股定理即可证明.
试题解析:(1)①补全图形,如图1
②判断: AE=BD
证明:如图2,连接AC,∵BA=BC,且∠ABC=60° ∴△ABC是等边三角形
∴∠ACB=60°,且CA=CB∵将线段CD绕点C顺时针旋转60°得到线段CE ∴CD=CE,且∠DCE=60°
∴∠BCD=∠ACE
∴△BCD≌△ACE(SAS) ∴AE=BD

(2)判断: ![]()
(3)判断: ![]()
证明:如图3,连接AC,∵BA=BC,且∠ABC=60°
∴△ABC是等边三角形,∴∠ACB=60°,且CA=CB
将线段CF绕点C顺时针旋转60°得到线段CE,连接EF、EA
∴CE=CF,且∠FCE=60°,∴△CEF是等边三角形
∴∠CFE=60°,且FE=FC,∴∠BCF=∠ACE
∴△BCF≌△ACE(SAS),∴AE=BF
∵∠AFC=150°, ∠CFE=60°,∴∠AFE=90°
在Rt△AEF中, 有: ![]()
∴![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定个人发表文章、出版图书所得稿费的纳税计算方法是:
①稿费不高于800元的不纳税;
②稿费高于800元,而低于4000元的应缴纳超过800元的那部分稿费的14%的税;
③稿费为4000元或高于4000元的应缴纳全部稿费的11%的税.
试根据上述纳税的计算方法作答:
(1)若王老师获得的稿费为2400元,则应纳税 元,若王老师获得的稿费为4000元,则应纳税 元;
(2)若王老师获稿费后纳税420元,求这笔稿费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】使两个直角三角形全等的条件是
A.一锐角对应相等B.两锐角对应相等
C.一条边对应相等D.两条边对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数的平方根有_________,它们的和为___________
-
科目: 来源: 题型:
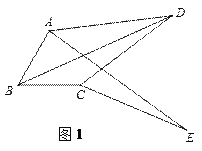
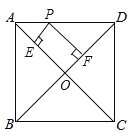
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=4,P是线段AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.2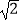
B.4
C.4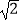
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
A.75°
B.70°
C.65°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】点P(m+3,m-2)在直角坐标系的x轴上,则点P的坐标为________.
相关试题

