【题目】如图,在正方形ABCD中,AB=4,P是线段AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )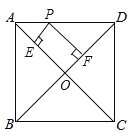
A.2![]()
B.4
C.4![]()
D.2
参考答案:
【答案】A
【解析】解:在正方形ABCD中,OA⊥OD,∠OAD=45°,
∵PE⊥AC,PF⊥BD,
∴四边形OEPF为矩形,△APE是等腰直角三角形,
∴PF=OE,PE=BE,
∴PE+PF=BE+OE=OA,
∵AB=BC=4,
∴OA=![]() AC=
AC=![]() x4
x4![]() =2
=2![]() ,
,
∴PE+PF=2![]() ,
,
故选A.
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】使两个直角三角形全等的条件是
A.一锐角对应相等B.两锐角对应相等
C.一条边对应相等D.两条边对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正数的平方根有_________,它们的和为___________
-
科目: 来源: 题型:
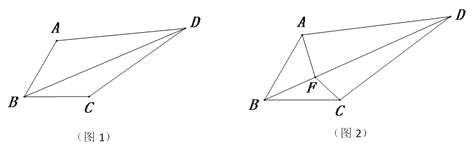
查看答案和解析>>【题目】如图1,在四边形ABCD中,BA=BC,∠ABC=60°,∠ADC=30°,连接对角线BD.
(1)将线段CD绕点C顺时针旋转60°得到线段CE,连接AE.
①依题意补全图1;
②试判断AE与BD的数量关系,并证明你的结论;
(2)在(1)的条件下,直接写出线段DA、DB和DC之间的数量关系;
(3)如图2,F是对角线BD上一点,且满足∠AFC=150°,连接FA和FC,探究线段FA、FB和FC之间的数量关系,并证明.
-
科目: 来源: 题型:
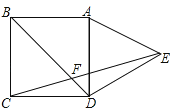
查看答案和解析>>【题目】如图,在正方形ABCD的外侧,作等边三角形ADE,连接CE,与对角线BD交于F,则∠BFC为( )
A.75°
B.70°
C.65°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】点P(m+3,m-2)在直角坐标系的x轴上,则点P的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线的顶点坐标为(1,2),且经过点(3,10)求这条抛物线的解析式.
相关试题

