【题目】在如图所示的七边形ABCDEFG中,∠1、∠2、∠3、∠4 四个角的外角和为180°,∠5 的外角为60°,BP、DP 分别平分∠ABC、∠CDE,则∠BPD 的度数是( )

A. 130° B. 120° C. 110° D. 100°
参考答案:
【答案】B
【解析】分析:根据邻补角互补得出,∠1+∠2+∠3+∠4=4×180°﹣180°=540°,∠5=120°,利用多边形内角和定理求出∠ABC+∠CDE=240°,根据角平分线定义得出∠CBP+∠CDP=120°,然后根据四边形内角和定理求出∠BPD 的度数.
详解:∵∠1、∠2、∠3、∠4 四个角的外角和为180°,∠5 的外角为60°,∴∠1+∠2+∠3+∠4=4×180°﹣180°=540°,∠5=120°,∴∠ABC+∠CDE=(7﹣2)×180°﹣540°﹣120°=240°.
∵BP、DP 分别平分∠ABC、∠CDE,∴∠CBP+∠CDP=![]() (∠ABC+∠CDE)=120°,∴∠BPD=360°﹣∠5﹣(∠CBP+∠CDP)=360°﹣120°﹣120°=120°.
(∠ABC+∠CDE)=120°,∴∠BPD=360°﹣∠5﹣(∠CBP+∠CDP)=360°﹣120°﹣120°=120°.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D、C、F,下列说法中,错误的是( )

A. △ABC中,AD是边BC上的高
B. △ABC中,GC是边BC上的高
C. △GBC中,GC是边BC上的高
D. △GBC中,CF是边BG上的高
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①
 ②
② ③
③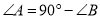 ④
④ 中,能确△ABC是直角三角形的定条件有
中,能确△ABC是直角三角形的定条件有A. ①② B. ③④ C. ①③④ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠B=∠C=65°,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )

A.

B.

C.
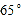
D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O直径,点C在⊙O上,
AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.
(1)求证:BD=BE;
(2)若DE=2,BD=
 ,求CE的长.
,求CE的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=20°,∠ABC与∠ACB的平分线交于点D1,∠ABD1与∠ACD1的平分线交于点D2,以此类推,∠ABD2与∠ACD2的平分线交于点D,则∠BDC的度数是__.

相关试题

