【题目】如图,△ABC中,∠B=∠C=65°,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )

A. ![]()
B. ![]()
C. ![]()
D. ![]()
参考答案:
【答案】C
【解析】
由条件AB=AC可以得出∠B=∠C,就可以得出△BDE≌△CFD,由△BDE≌△CFD,推出∠BED=∠CDF,∠BDE=∠CFD,由平角的定义就可以得出∠EDF=∠B,进而可求出∠B的度数即可解决问题;
∵AB=AC,
∴∠B=∠C,
在△BDE和△CFD中
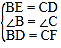 ,
,
∴△BDE≌△CFD(SAS),
∴∠BED=∠CDF,∠BDE=∠CFD,
∴∠BED+∠BDE=∠CDF+∠CFD,
∵∠BED+∠BDE+∠B=∠CDF+∠CFD+∠EDF=180°,
∴∠B=∠EDF,
∵∠B=![]() (180°﹣50°)=65°
(180°﹣50°)=65°
∴∠DEF=∠B=65°.
故选:C.
-
科目: 来源: 题型:
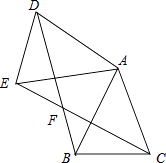
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点顺时针方向旋转得到△ADE,连接BD,CE交于点F,求证:△AEC≌△ADB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某市12000名初中学生的视力情况,该校数学兴趣小组从该市七、八、九年级各随机抽取了100名学生进行调查,整理他们的视力情况数据,得到如下的折线统计图.

(1)由统计图可以看出年级越高视力不良率越(填“高”或“低”);
(2)抽取的八年级学生中,视力不良的学生有名;
(3)请你根据抽样调查的结果,估计该市12000名初中学生中视力不良的人数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】只给定三角形的两个元素,画出的三角形的形状和大小是不确定的,在下列给定的两个条件上增加一个“AB=5cm”的条件后,所画出的三角形的形状和大小仍不能完全确定的是( )
A.
 ,
,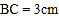 B.
B.  ,
,
C.
 ,
, D.
D. 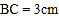 ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA的方向是北偏东20,射线OB的方向是北偏西40,OD是OB的反向延长线,OC是∠AOD的平分线。
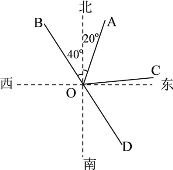
(1)求∠BOC的度数;
(2)求出射线OC的方向。
-
科目: 来源: 题型:
查看答案和解析>>【题目】保护视力要求人写字时眼睛和笔端的距离应超过30cm,图1是一位同学的坐姿,把他的眼睛B,肘关节C和笔端A的位置关系抽象成图2的△ABC,已知BC=30cm,AC=22cm,∠ACB=53°,他的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
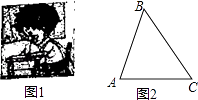
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们都知道,|4―(―2)|表示4与-2的差的绝对值,实际上也可以理解为4与-2两数在数轴上所对应的两点之间的距离;同理|x―3|也可以理解为x与3两数在数轴上所对应的两点之间的距离,试探索并完成填空。
(1)求|8―(―3)|= ;|-3―5|= 。
(2)如图,x是0到4之间(包括0,4)的一个数,那么|x―1|+|x―2|+|x―3|+|x―4|的最小值等于多少?
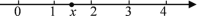
相关试题

