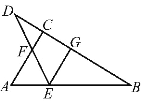
【题目】如图,在Rt△ABC中,∠ACB=90°,D是BC延长线上的一点,线段BD的垂直平分线EG交AB于点E,交BD于点G.
(1)当∠B=30°时,AE和EF有什么关系?请说明理由.
(2)当点D在BC的延长线上(CD<BC)运动时,点E是否在线段AF的垂直平分线上?
参考答案:
【答案】(1)AE=EF(2)点E是在线段AF的垂直平分线上
【解析】
(1)根据线段垂直平分线性质得出DE=BE,求出∠D=∠B=30°,根据三角形内角和定理和三角形外角性质求出∠A=∠DEA=60°,即可得出答案.
(2)求出∠A=∠AFE,根据线段垂直平分线性质得出即可.
解:
(1)AE=EF.理由如下:
∵线段BD的垂直平分线EG交AB于点E,交BD于点G,
∴DE=BE,
∵∠B=30°,
∴∠D=∠B=30°,
∴∠DEA=∠D+∠B=60°,
∵在Rt△ABC中,∠ACB=90°,∠B=30°,
∴∠A=60°,
∴∠A=∠DEA=60°,
∴△AEF是等边三角形,
∴AE=EF.
(2)点E是在线段AF的垂直平分线上.理由如下:
∵∠B=∠D,∠ACB=90°=∠FCD,
∴∠A=∠DFC,
∵∠DFC=∠AFE,
∴∠A=∠AFE,
∴EF=AE,
∴点E在线段AF的垂直平分线上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的是
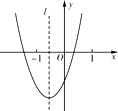
A.a<0
B.c>0
C.a+b+c>0
D.b2-4ac<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线:y=ax2+bx+c(a>0)经过A(﹣1,1),B(2,4)两点,顶点坐标为(m,n),有下列结论: ①b<1;②c<2;③0<m<
 ;④n≤1.
;④n≤1.
则所有正确结论的序号是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】(1计算:
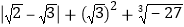 ;
;(2)解不等式组
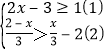
请结合题意填空,完成本题的解答:
解不等式(1),得______________.
解不等式(2),得_______________.
把不等式(1)和(2)的解集在数轴上表示出来

∴原不等式组的解集为_________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校1200名学生参加了一场“安全知识”问答竞赛活动,为了解笔试情况,随机抽查了部分学生的得分情况,整理并制作了如图所示的图表(部分未完成),请根据图表提供的信息,解答下列问题:
分数段
频数
频率

30
0.1

90



0.4

60
0.2
(Ⅰ)本次调查的样本容量为______;
(Ⅱ)在表中,
 ______,
______, ______;
______;(Ⅲ)补全频数分布直方图;

(Ⅳ)如果比赛成绩80分以上(含80分)为优秀,本次竞赛中笔试成绩为优秀的大约有多少名学生?
-
科目: 来源: 题型:
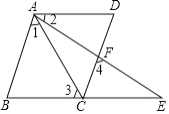
查看答案和解析>>【题目】填空:已知:如图,
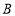 、
、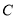 、
、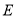 三点在同一直线上,
三点在同一直线上,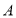 、
、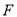 、
、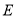 三点在同一直线上,
三点在同一直线上, ,
, .求证:
.求证: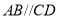 .
.
证明:∵
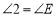
∴________(内错角相等,两直线平行)
∴
 ________(两直线平行,内错角相等)
________(两直线平行,内错角相等)∵

∴
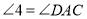 (________________)
(________________)∵
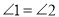
∴
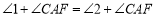 ,(________________)
,(________________)即
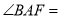 ________
________∴

∴
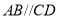 (同位角相等,两直线平行).
(同位角相等,两直线平行). -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了庆祝校园艺术节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花一共需13元,2盆A种花和1盆B种花一共需11元.
(1)求1盆A种花和1盒B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
相关试题

