【题目】如图,边长为 7 的正方形 OABC 放置在平面直角坐标系中,动点 P 从点 C 出发,以 每秒 1 个单位的速度向 O 运动,点 Q 从点 O 同时出发,以每秒 1 个单位的速度向点 A 运动,到达端点即停止运动,运动时间为 t 秒,连 PQ、BP、BQ.
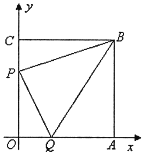
(1)写出 B 点的坐标;
(2)填写下表:
时间 t(单位:秒) | 1 | 2 | 3 | 4 | 5 | 6 |
OP 的长度 | ||||||
OQ 的长度 | ||||||
PQ 的长度 | ||||||
四边形 OPBQ 的面积 |
①根据你所填数据,请描述线段 PQ 的长度的变化规律?并猜测 PQ 长度的最小值.
②根据你所填数据,请问四边形 OPBQ 的面积是否会发生变化?并证明你的论断;
(3)设点 M、N 分别是 BP、BQ 的中点,写出点 M,N 的坐标,是否存在经过 M, N 两点的反比例函数?如果存在,求出 t 的值;如果不存在,说明理由.
参考答案:
【答案】(1)B(7,7);(2)表格填写见解析;①,PQ长度的最小值是![]() ;
;
②四边形OPBQ的面积不会发生变化;(3)t=3.5存在经过M,N两点的反比例函数.
【解析】
通过写点的坐标,填表,搞清楚本题的基本数量关系,每个量的变化规律,然后进行猜想;用运动时间t,表示线段OP,OQ,CP,AQ的长度,运用割补法求四边形OPBQ的面积,由中位线定理得点M(3.5,7-![]() ),N(
),N(![]() ,3.5),反比例函数图象上点的坐标特点是
,3.5),反比例函数图象上点的坐标特点是![]() ,利用该等式求t值.
,利用该等式求t值.
解:(1)∵在正方形 OABC中OA=OC=7
∴B(7,7)
(2)表格填写如下:
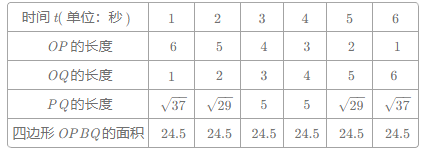
①线段PQ的长度的变化规律是先减小再增大,PQ长度的最小值是![]() .理由如下:
.理由如下:
在Rt△POQ中,OP=7-t,OQ=t
∴PQ2=(7-t)2+t2=2t2-14t+49=![]()
∵![]()
∴![]()
∴当![]() 时PQ2最取得最小值为
时PQ2最取得最小值为![]()
∴此时![]()
②根据所填数据,四边形OPBQ的面积不会发生变化;
∵![]() =24.5,
=24.5,
∴四边形OPBQ的面积不会发生变化.
(3)点M(3.5,7![]() ),N(
),N(![]() ,3.5),
,3.5),
当3.5(7![]() )=
)=![]() ×3.5时,则t=3.5,
×3.5时,则t=3.5,
∴当t=3.5存在经过M,N两点的反比例函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小马虎做一道数学题,“已知两个多项式
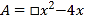 ,
,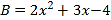 ,试求
,试求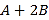 .”其中多项式
.”其中多项式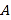 的二次项系数印刷不清楚.
的二次项系数印刷不清楚.(1)小马虎看答案以后知道
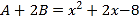 ,请你替小马虎求出系数“
,请你替小马虎求出系数“ ”;
”;(2)在(1)的基础上,小马虎已经将多项式
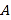 正确求出,老师又给出了一个多项式
正确求出,老师又给出了一个多项式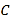 ,要求小马虎求出
,要求小马虎求出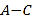 的结果.小马虎在求解时,误把“
的结果.小马虎在求解时,误把“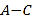 ”看成“
”看成“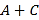 ”,结果求出的答案为
”,结果求出的答案为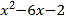 .请你替小马虎求出“
.请你替小马虎求出“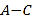 ”的正确答案.
”的正确答案. -
科目: 来源: 题型:
查看答案和解析>>【题目】一次期中考试中,甲、乙、丙、丁、戍五位同学的数学、英语成绩等有关信息如下 表所示:(单位:分)
甲
乙
丙
丁
戍
平均分
标准差
数学
71
72
69
68
70
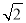
英语
88
82
94
85
76
85
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择.标准分 的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.从标准分看, 标准分大的考试成绩更好.请问甲同学在本次考试中,数学与英语哪个学科考 得更好?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为
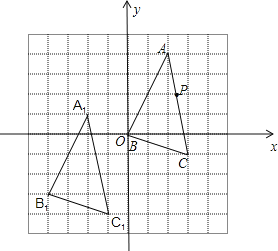
A.(1.4,-1) B.(1.5,2) C.(1.6,1) D.(2.4,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判定中,正确的个数有( )
①一组对边平行,一组对边相等的四边形是平行四边形;
②对角线互相平分且相等的四边形是矩形;
③对角线互相垂直的四边形是菱形;
④对角线互相垂直平分且相等的四边形是正方形,
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( ) .
A. 对角线相等的四边形是矩形;
B. 对角线互相垂直的四边形是菱形;
C. 对角线互相平分的四边形是平行四边形;
D. 对角线互相垂直平分的四边形是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=- (x-2)2+7,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( )
A. 2 B.
 C.
C.  D.
D. 
相关试题

