【题目】二次函数y=- (x-2)2+7,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】分析:条件m≤x≤n和mn<0可得m<0,n>0,
所以y的最小值为2m为负数,最大值为2n为正数.
最大值为2n分两种情况,(1)顶点纵坐标取到最大值,求出n=3.5,结合图象最小值只能由x=m时求出.
(2)顶点纵坐标取不到最大值,结合图象最大值只能由x=n求出,最小值只能由x=m求出.
详解:二次函数y=﹣(x﹣2)2+7的大致图象如下:
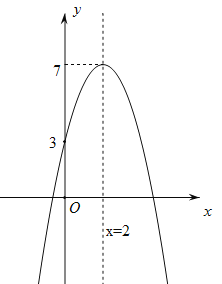 .
.
①当m≤0≤x≤n<2时,当x=m时y取最小值,即2m=﹣(m﹣2)2+7,解得:m=-1,或m=3(舍去).
当x=n时y取最大值,即2n=﹣(n﹣2)2+7,解得:n=-1或n=3(均不符合题意,舍去);
②当m≤0≤x≤2≤n时,当x=m时y取最小值,即2m=﹣(m﹣2)2+7,解得:m=-1,或m=3(舍去).
当x=2时y取最大值,即2n=﹣(2﹣2)2+7,解得:n=![]() ,
,
或x=n时y取最小值,x=2时y取最大值,2m=﹣(n﹣2)2+7,n=![]() ,∴m=
,∴m=![]() .
.
∵m<0,∴此种情形不合题意,
综上所述:m=-1,n=![]() ,m+n=﹣1+
,m+n=﹣1+![]() =
=![]() .
.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为 7 的正方形 OABC 放置在平面直角坐标系中,动点 P 从点 C 出发,以 每秒 1 个单位的速度向 O 运动,点 Q 从点 O 同时出发,以每秒 1 个单位的速度向点 A 运动,到达端点即停止运动,运动时间为 t 秒,连 PQ、BP、BQ.
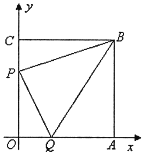
(1)写出 B 点的坐标;
(2)填写下表:
时间 t(单位:秒)
1
2
3
4
5
6
OP 的长度
OQ 的长度
PQ 的长度
四边形 OPBQ 的面积
①根据你所填数据,请描述线段 PQ 的长度的变化规律?并猜测 PQ 长度的最小值.
②根据你所填数据,请问四边形 OPBQ 的面积是否会发生变化?并证明你的论断;
(3)设点 M、N 分别是 BP、BQ 的中点,写出点 M,N 的坐标,是否存在经过 M, N 两点的反比例函数?如果存在,求出 t 的值;如果不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判定中,正确的个数有( )
①一组对边平行,一组对边相等的四边形是平行四边形;
②对角线互相平分且相等的四边形是矩形;
③对角线互相垂直的四边形是菱形;
④对角线互相垂直平分且相等的四边形是正方形,
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( ) .
A. 对角线相等的四边形是矩形;
B. 对角线互相垂直的四边形是菱形;
C. 对角线互相平分的四边形是平行四边形;
D. 对角线互相垂直平分的四边形是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有两个一元二次方程:M:ax2+bx+c=0,N:cx2+bx+a=0,其中a+c=0,以下列四个结论中正确的是_____(填写序号).
①如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
②如果方程M有两根符号相同,那么方程N的两根符号也相同;
③如果方程M和方程N有一个相同的根,那么这个根必是x=1;
④如果5是方程M的一个根,那么
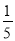 是方程N的一个根.
是方程N的一个根. -
科目: 来源: 题型:
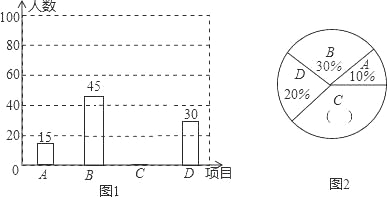
查看答案和解析>>【题目】为进一步推广“阳光体育”大课间活动,某中学对已开设的A实心球,B立定跳远,C跑步,D跳绳四种活动项目的学生喜欢情况进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2的统计图,请结合图中的信息解答下列问题:
(1)请计算本次调查中喜欢“跑步”的学生人数和所占百分比,并将两个统计图补充完整;
(2)随机抽取了5名喜欢“跑步”的学生,其中有3名女生,2名男生,现从这5名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为E.
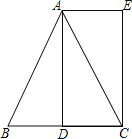
(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.
相关试题

