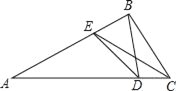
【题目】如图,在△ABC中,∠ABC=100°,∠ACB的平分线交AB边于点E,在AC边取点D,使∠CBD=20°,连接DE,则∠CED的大小=_____(度).
参考答案:
【答案】10.
【解析】
由CE是∠ACB的平分线,可得![]() 由三角形外角的性质,可得∠ADB=∠CBD+∠BCD ①,∠ADE=∠CED+∠ACE ②,继而求得答案.
由三角形外角的性质,可得∠ADB=∠CBD+∠BCD ①,∠ADE=∠CED+∠ACE ②,继而求得答案.
解:延长CB到F,
∵在△ABC中,∠ABC=100°,∠CBD=20°,
∴∠ABF=80°,∠ABD=80°,
∴AB平分∠FBD,
又∵∠ACB的平分线交AB边于点E,
∴点E到边BF,BD,AC的距离相等,
∴点E在∠ADB的平分线上,
即DE平分∠ADB,
∴CE是∠ACB的平分线,
∴![]()
∠ADB是![]() 的外角,∠ADE是
的外角,∠ADE是![]() 的外角,
的外角,
∴∠ADB=∠CBD+∠BCD①,∠ADE=∠CED+∠ACE②
∴①②×2得:2∠CED=∠CBD
∴![]()
故答案为:10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上A 点对应的数为﹣5,B 点在A 点右边,电子蚂蚁甲、乙在B分别以2个单位/秒、1个单位/秒的速度向左运动,电子蚂蚁丙在A 以3个单位/秒的速度向右运动.
(1)若电子蚂蚁丙经过5秒运动到C 点,求C 点表示的数;

(2)若它们同时出发,若丙在遇到甲后1秒遇到乙,求B 点表示的数;

(3)在(2)的条件下,设它们同时出发的时间为t 秒,是否存在t的值,使丙到乙的距离是丙到甲的距离的2倍?若存在,求出t 值;若不存在,说明理由.

-
科目: 来源: 题型:
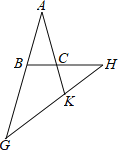
查看答案和解析>>【题目】如图,△ABC中,AB=AC,分别在AB,BC的延长线上截取点G,H,使BG=BH,延长AC交GH于点K,且AK=KG,则∠BAC的大小等于( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
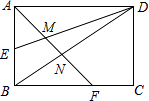
查看答案和解析>>【题目】如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
A.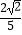
B.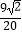
C.
D.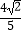
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备在七年级举办百科知识竞赛,在张贴规则宣传之后,为了解学生对这次竞赛的了解程度,在全校400名七年级学生中随机抽取部分学生迸行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅统计图.
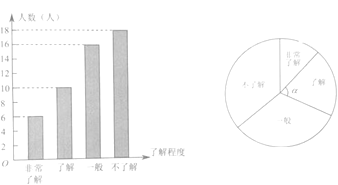
(1)抽取调查的学生人数是_____人;
(2)扇形统计图中“了解”对应的圆心角α的度数是_____度;
(3)全校七年级学生中对这次竞赛“非常了解”的大约有 人。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=
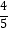 ,反比例函数y=
,反比例函数y=  在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( ) 
A.60
B.80
C.30
D.40 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC,过边AB上一点N作AB的垂线交BC于点M.
(1)如图1,若∠A=40°,求∠NMB的度数.
(2)如图2,若∠A=70°,求∠NMB的度数.
(3)你可以再分别给出几个∠A(∠A为锐角)的度数,你发现规律了吗?写出当∠A为锐角时,你猜想出的规律,并进行证明.
(4)当∠A为直角、钝角时,是否还有(3)中的结论(直接写出答案).

相关试题

