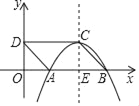
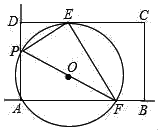
【题目】如图,ABCD位于直角坐标系中,AB=2,点D(0,1),以点C为顶点的抛物线y=ax2+bx+c经过x轴正半轴上的点A,B,CE⊥x轴于点E.
(1)求点A,B,C的坐标.
(2)将该抛物线向上平移m个单位恰好经过点D,且这时新抛物线交x轴于点M,N.
①求MN的长.
②点P是新抛物线对称轴上一动点,将线段AP绕点A顺时针旋转60°得AQ,则OQ的最小值为 (直接写出答案即可)
参考答案:
【答案】(1)A(1,0),B(3,0),C(2,1);(2)①MN=![]() ;②
;② ![]()
【解析】
(1)由ABCD可知CD,进而求出E和C点坐标,由AB长从而求出AB点.(2)①由第一问解出抛物线方程,上移m更改抛物线方程,由其过D,进而求出上移后抛物线方程,再求MN.②根据三角函数,求出最小值.
(1)∵四边形ABCD是平行四边形,
∴CD=AB=2,
∵CE⊥x轴,
∴OE=2,
∵点E是AB中点,
∴AE=BE=1,
∴OA=2﹣1=1.OB=OE+BE=3,
∴A(1,0),B(3,0),
∵D(0,1),
∴C(2,1);
(2)由(1)知,抛物线的顶点C(2,1),
∴设抛物线的解析式为y=a(x﹣2)2+1,
∵A(1,0)在抛物线上,
∴a(1﹣2)2+1=0,
∴a=﹣1,
∴抛物线解析式为y=﹣(x﹣2)2+1,
①该抛物线向上平移m个单位恰好经过点D,设平移后的抛物线解析式为y=﹣(x﹣2)2+1+m,
∵D(0,1),
∴﹣(﹣2)2+1+m=1,
∴m=4,
∴平移后的抛物线解析式为y=﹣(x﹣2)2+5,
令y=0,
∴0=﹣(x﹣2)2+5,
∴x=2±![]() ,
,
∴M(2+![]() ,0),N(2﹣
,0),N(2﹣![]() ,0),
,0),
∴MN=2![]() ;
;
②如图,
在第一象限的抛物线对称轴上取一点P1,使∠P1AB=60°,
在Rt△AEP1中,AP1=2AE=2,P2E=![]()
∴点Q1和点B重合,
∴Q1(3,0),P1(2,![]() ),
),
在第一象限的抛物线对称轴上取一点P2,使∠P2AB=30°,
在Rt△AEP2中,P2E=AEtan30°=![]() ,
,
∴点Q2(2,﹣![]() ),
),
∴直线Q1Q2的解析式y=![]() x﹣
x﹣![]()
在第二象限的抛物线对称轴上取一点P3,使∠P3AE=60°,
由旋转知,Q3和点P1关于点A对称,
∴Q3(0,﹣![]() ),
),
∴点Q3在直线Q1Q2上,
∴点Q的运动轨迹是直线Q1Q2,
∴当OQ⊥Q1Q2时,OD最短,
∵Q1Q3=2![]()
∴OD最小==![]() ,
,
故答案为![]() .
.
-
科目: 来源: 题型:
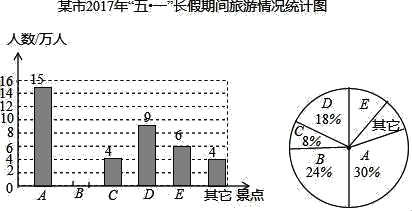
查看答案和解析>>【题目】随着道路交通的不断完善,某市旅游业快速发展,该市旅游景区有A、B、C、D、E等著名景点,市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图(不完整)如下所示,根据相关信息解答下列问题:
(1)2017年“五一”期间,该市旅游景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)在等可能性的情况下,甲、乙两个旅行团在A、B、D三个景点中选择去同一景点的概率是多少?请用画树状图或列表加以说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ ABC中,AB = AC

(1)如图 1,如果∠BAD = 30°,AD是BC上的高,AD =AE,则∠EDC =
(2)如图 2,如果∠BAD = 40°,AD是BC上的高,AD = AE,则∠EDC =
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:
(4)如图 3,如果AD不是BC上的高,AD = AE,是否仍有上述关系?如有,请你写出来,并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,钝角△ABC中,AB=AC,BC=2
 ,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.
,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.(1)求证:EF⊥AC.
(2)连结DF,若∠ABC=30°,且DF∥BC,求⊙O的半径长.

-
科目: 来源: 题型:
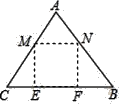
查看答案和解析>>【题目】如图,王爷爷家院子里有一块三角形田地ABC,AB=AC=5米,BC=6米,现打算把它开垦出一个矩形MNFE区域种植韭菜,△AMN区域种植芹菜,△CME和△BNF区域种植青菜(开垦土地面积损耗均忽略不计),其中点M,N分别在AC,AB上,点E,F在BC上,已知韭菜每平方米收益100元,芹菜每平方米收益60元,青菜每平方米收益40元,设CM=5x米,王爷爷的蔬菜总收益为W元.
(1)当矩形MNFE恰好为正方形时,求韭菜种植区域矩形MNFE的面积.
(2)若种植韭菜的收益等于另两种蔬菜收益之和的2倍,求这时x的值.
(3)求王爷爷的蔬菜总收益为W关于x的函数表达式及W的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AD=10,CD=15,E是边CD上一点,且DE=5,P是射线AD上一动点,过A,P,E三点的⊙O交直线AB于点F,连结PE,EF,PF,设AP=m.
(1)当m=6时,求AF的长.
(2)在点P的整个运动过程中.
①tan∠PFE的值是否改变?若不变,求出它的值;若改变,求出它的变化范围.
②当矩形ABCD恰好有2个顶点落在⊙O上时,求m的值.
(3)若点A,H关于点O成中心对称,连结EH,CH.当△CEH是等腰三角形时,求出所有符合条件的m的值.(直接写出答案即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
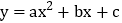 的图象如图所示,下列结论错误的是( )
的图象如图所示,下列结论错误的是( )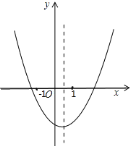
A. b2-4ac>0 B. a-b+c<0 C. abc<0 D. 2a+b>0
相关试题

