【题目】在△ ABC中,AB = AC

(1)如图 1,如果∠BAD = 30°,AD是BC上的高,AD =AE,则∠EDC =
(2)如图 2,如果∠BAD = 40°,AD是BC上的高,AD = AE,则∠EDC =
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:
(4)如图 3,如果AD不是BC上的高,AD = AE,是否仍有上述关系?如有,请你写出来,并说明理由
参考答案:
【答案】(1)15°;(2)20°;(3)∠BAD=2∠EDC;(4)成立,理由见解析
【解析】
(1)根据等腰三角形三线合一,可知∠DAE=30°,再根据AD=AE,可求∠ADE的度数,从而可知答案;
(2)同理易知答案;
(3)通过(1)(2)题的结论可知∠BAD=2∠EDC,
(4)由于AD=AE,所以∠ADE=∠AED,根据已知容易证得∠BAD=2∠EDC.
解:(1)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD=30°
∵AD=AE,
∴![]()
∴∠DEC=90°-∠AD =15°;
(2)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD=40°
∵AD=AE,
∴![]()
∴∠DEC=90°-∠ADE=20°;
(3)根据前两问可知:∠BAD=2∠EDC
(4)仍成立,理由如下:
∵AD=AE,
∴∠ADE=∠AED
∵∠BAD+∠B=∠ADC,∠ADC=∠ADE+∠EDC
∴∠ADC=∠AED+∠EDC
∵∠AED=∠EDC+∠C
∴∠ADC=(∠EDC+∠C)+∠EDC=2∠EDC+∠C
又∵AB=AC
∴∠B=∠C
∴∠BAD=2∠EDC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系xOy中,直线y=﹣x+b分别交x,y轴的正半轴于点A,B,交反比例函数y=﹣
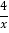 的图象于点C,D(点C在第二象限内),过点C作CE⊥x轴于点E,记四边形OBCE的面积为S1,△OBD的面积为S2,若
的图象于点C,D(点C在第二象限内),过点C作CE⊥x轴于点E,记四边形OBCE的面积为S1,△OBD的面积为S2,若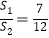 ,则CD的长为____.
,则CD的长为____.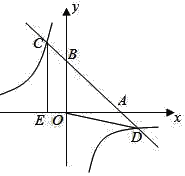
-
科目: 来源: 题型:
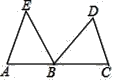
查看答案和解析>>【题目】如图,在△ABE中,C为边AB延长线上一点,BC=AE,点D在∠EBC内部,且∠EBD=∠A=∠DCB.
(1)求证:△ABE≌△CDB.
(2)连结DE,若∠CDB=60°,∠AEB=50°,求∠BDE的度数.
-
科目: 来源: 题型:
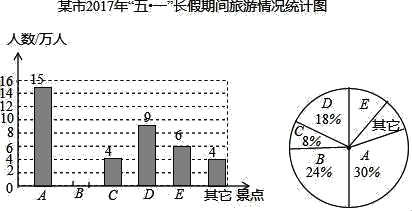
查看答案和解析>>【题目】随着道路交通的不断完善,某市旅游业快速发展,该市旅游景区有A、B、C、D、E等著名景点,市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图(不完整)如下所示,根据相关信息解答下列问题:
(1)2017年“五一”期间,该市旅游景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)在等可能性的情况下,甲、乙两个旅行团在A、B、D三个景点中选择去同一景点的概率是多少?请用画树状图或列表加以说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,钝角△ABC中,AB=AC,BC=2
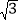 ,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.
,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.(1)求证:EF⊥AC.
(2)连结DF,若∠ABC=30°,且DF∥BC,求⊙O的半径长.

-
科目: 来源: 题型:
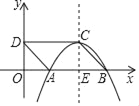
查看答案和解析>>【题目】如图,ABCD位于直角坐标系中,AB=2,点D(0,1),以点C为顶点的抛物线y=ax2+bx+c经过x轴正半轴上的点A,B,CE⊥x轴于点E.
(1)求点A,B,C的坐标.
(2)将该抛物线向上平移m个单位恰好经过点D,且这时新抛物线交x轴于点M,N.
①求MN的长.
②点P是新抛物线对称轴上一动点,将线段AP绕点A顺时针旋转60°得AQ,则OQ的最小值为 (直接写出答案即可)
-
科目: 来源: 题型:
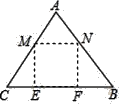
查看答案和解析>>【题目】如图,王爷爷家院子里有一块三角形田地ABC,AB=AC=5米,BC=6米,现打算把它开垦出一个矩形MNFE区域种植韭菜,△AMN区域种植芹菜,△CME和△BNF区域种植青菜(开垦土地面积损耗均忽略不计),其中点M,N分别在AC,AB上,点E,F在BC上,已知韭菜每平方米收益100元,芹菜每平方米收益60元,青菜每平方米收益40元,设CM=5x米,王爷爷的蔬菜总收益为W元.
(1)当矩形MNFE恰好为正方形时,求韭菜种植区域矩形MNFE的面积.
(2)若种植韭菜的收益等于另两种蔬菜收益之和的2倍,求这时x的值.
(3)求王爷爷的蔬菜总收益为W关于x的函数表达式及W的最大值.
相关试题

