【题目】如下表,方程1、方程2、方程3…是按照一定规律排列的一列方程。
(1)猜想方程1的解,并将它们的解填在表中的空白处。
序号 | 方程 | 方程的解( |
1 |
|
|
2 |
|
|
3 |
|
|
… | …… | …… |
(2)若方程![]()
![]() 的解是
的解是![]() ,猜想a,b的值。
,猜想a,b的值。
(3)请写出这列方程中的第n个方程和它的解。
参考答案:
【答案】(1)3,4;(2)a=12,b=5;(3)第n个方程为![]() ﹣
﹣![]() =1,它的解为x1=n+2,x2=2n+2.
=1,它的解为x1=n+2,x2=2n+2.
【解析】
(1)根据表格中方程解的特征判断出所求即可;
(2)根据表格中的规律确定出a与b的值即可;
(3)归纳总结得到一般性规律,写出即可.
解:(1)填写如下:
序号 | 方程 | 方程的解(x1<x2) |
1 |
| x1=3,x2=4 |
2 |
| x1=4,x2=6 |
3 |
| x1=5,x2=8 |
…… | …… | …… |
故答案为:3,4;
(2)若方程![]() ﹣
﹣![]() =1(a>b)的解是x1=6,x2=10,则有a=12,b=5;
=1(a>b)的解是x1=6,x2=10,则有a=12,b=5;
(3)归纳得:第n个方程为![]() ﹣
﹣![]() =1,它的解为x1=n+2,x2=2n+2.
=1,它的解为x1=n+2,x2=2n+2.
-
科目: 来源: 题型:
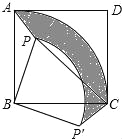
查看答案和解析>>【题目】已知,点P是正方形ABCD内的一点,连接PA,PB,PC.将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图).
(1)设AB的长为a,PB的长为b(b<a),求△PAB旋转到△P′CB的过程中边PA所扫过区域(图中阴影部分)的面积;
(2)若PA=2,PB=4,∠APB=135°,求PC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹)
(2)求残片所在圆的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与半圆O相切时(如图①),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如图②),设另一交点为E,连接AE,若AE∥OC,
①AE与OD的大小有什么关系?为什么?
②求∠ODC的度数.
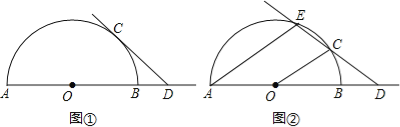
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是边长为1的正方形,
是边长为1的正方形, 与
与 轴正半轴的夹角为15°,点
轴正半轴的夹角为15°,点 在抛物线
在抛物线 的图象上,则
的图象上,则 的值为( )
的值为( )
A.
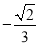 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读理解:课外兴趣小组活动时,老师提出了如下问题:
在△ABC中,AB=9,AC=5,求BC边上的中线AD的取值范围。
小明在组内经过合作交流,得到了如下的解决方法(如图1):
①延长AD到Q,使得DQ=AD;
②再连接BQ,把AB、AC、2AD集中在△ABQ中;
③利用三角形的三边关系可得4<AQ<14,则AD的取值范围是_____________。
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的己知条件和所求证的结论集中到同一个三角形中。
(2)请你写出图1中AC与BQ的位置关系并证明。
(3)思考:已知,如图2,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠FAC=90°。试探究线段AD与EF的数量和位置关系并加以证明。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能写成
 的形式(其中a,b均为自然数),则称之为婆罗摩笈多数,比如7和31均是婆罗摩笈多数,因为7=22+3×12,31=22+3×32。
的形式(其中a,b均为自然数),则称之为婆罗摩笈多数,比如7和31均是婆罗摩笈多数,因为7=22+3×12,31=22+3×32。(1)请证明:28和217都是婆罗摩笈多数。
(2)请证明:任何两个婆罗摩笈多数的乘积依旧是婆罗摩笈多数。
相关试题

