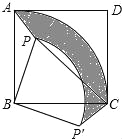
【题目】已知,点P是正方形ABCD内的一点,连接PA,PB,PC.将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图).
(1)设AB的长为a,PB的长为b(b<a),求△PAB旋转到△P′CB的过程中边PA所扫过区域(图中阴影部分)的面积;
(2)若PA=2,PB=4,∠APB=135°,求PC的长.
参考答案:
【答案】(1)![]() (a2-b2);(2)6.
(a2-b2);(2)6.
【解析】
试题分析:(1)依题意,将△P′CB逆时针旋转90°可与△PAB重合,此时阴影部分面积=扇形BAC的面积-扇形BPP'的面积,根据旋转的性质可知,两个扇形的中心角都是90°,可据此求出阴影部分的面积.
(2)连接PP',根据旋转的性质可知:BP=BP',旋转角∠PBP'=90°,则△PBP'是等腰直角三角形,∠BP'C=∠BPA=135°,∠PP'C=∠BP'C-∠BP'P=135°-45°=90°,可推出△PP'C是直角三角形,进而可根据勾股定理求出PC的长.
试题解析:(1)∵将△PAB绕点B顺时针旋转90°到△P′CB的位置,
∴△PAB≌△P'CB,
∴S△PAB=S△P'CB,
S阴影=S扇形BAC-S扇形BPP′=![]() (a2-b2);
(a2-b2);
(2)连接PP′,根据旋转的性质可知:△APB≌△CP′B,
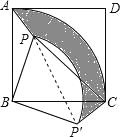
∴BP=BP′=4,P′C=PA=2,∠PBP′=90°,
∴△PBP'是等腰直角三角形,P'P2=PB2+P'B2=32;
又∵∠BP′C=∠BPA=135°,
∴∠PP′C=∠BP′C-∠BP′P=135°-45°=90°,即△PP′C是直角三角形.
PC=![]() =6.
=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣2(x+1)2+3的顶点坐标是( )
A.(1,3) B.(﹣1,﹣3) C.(﹣2,3) D.(﹣1,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x-2的平方根是±2,2x+y+7的立方根是3,求x2+y2的平方根
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( ).
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=2
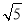 ,求⊙O的半径.
,求⊙O的半径.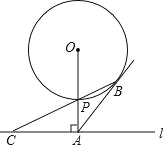
-
科目: 来源: 题型:
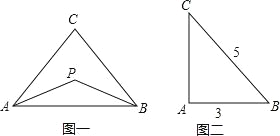
查看答案和解析>>【题目】定义:到三角形两个顶点距离相等的点,叫做此三角形的准外心,如图,若PA=PB,则点P为△ABC的准外心,已知,如图,在△ABC中,∠A为直角,BC=5,AB=3.
(1)若△ABC的一个准外心P在AC边上,试用尺规找出点P的位置(保留痕迹,不写作法);
(2)求线段PA的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>b,则下列不等关系中正确的是
A. ac>bcB. a+c2>b+c2C. a-1>b+1D. ac2>bc2
相关试题

