【题目】已知点A(1,a)是直线y1=2x与双曲线y2=![]() 在第一象限的交点.
在第一象限的交点.
(1)求双曲线的解析式;
(2)直接写出当y1>y2时,自变量的取值范围.
参考答案:
【答案】(1)y2=![]() ;(2)x>1或-1<x<0.
;(2)x>1或-1<x<0.
【解析】
(1)先求出点A的坐标,再根据待定系数法,即可得到答案;
(2)联立y1=2x,y2=![]() ,求出函数图象的另一个交点坐标,结合函数图象,即可得到答案.
,求出函数图象的另一个交点坐标,结合函数图象,即可得到答案.
(1)∵点A(1,a)是直线y1=2x与双曲线y2=![]() 在第一象限的交点.
在第一象限的交点.
∴点A(1,a)代入y1=2x得:a=2×1=2,
∴A(1,2),
∴2=![]() ,即:k=2,
,即:k=2,
∴双曲线的解析式为:y2=![]() ;
;
(2)联立y1=2x,y2=![]() ,得:2x=
,得:2x=![]() ,解得:x=±1,
,解得:x=±1,
∴直线y1=2x与双曲线y2=![]() 的交点坐标为:(1,2),(-1,-2),函数图象如图所示:
的交点坐标为:(1,2),(-1,-2),函数图象如图所示:
∴当x>1或-1<x<0时,y1>y2,
∴当y1>y2时,自变量的取值范围为:x>1或-1<x<0.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(a+b)x2+2cx+(b-a)=0,其中a、b、c分别为
 三边的长.
三边的长.(1)如果
 是方程的根,试判断
是方程的根,试判断 的形状,并说明理由.
的形状,并说明理由.(2)如果方程有两个相等的实数根,试判断
 的形状,并说明理由.
的形状,并说明理由. (3)如果
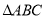 是等边三角形,试求这个一元二次方程的根.
是等边三角形,试求这个一元二次方程的根. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣
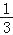 x+1与y轴交于点D.
x+1与y轴交于点D.
(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
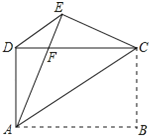
(1)求证:△DEC≌△EDA;
(2)求DF的值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列给出的条件中,能判定四边形ABCD为平行四边形的是()
A.AB=BC,CD=DAB.AB//CD,AD=BC
C.AB//CD,∠A=∠CD.∠A=∠B,∠C=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在RtΔABC中,∠C=90°,∠BAC的角平分线AD交BC边于D,以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D,与AB边的另一个交点为E.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为4,∠B=30°.求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD,AB=10,BC=13,点P为边AD上一动点,点A’与点A关于BP对称,连结A’C,当△A’BC为等腰三角形时,AP的长度为()

A.2B.
 C.2或
C.2或 D.2或
D.2或
相关试题

