【题目】如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
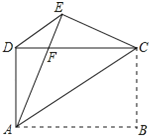
(1)求证:△DEC≌△EDA;
(2)求DF的值;
参考答案:
【答案】见解析
【解析】
试题(1)由矩形和翻折的性质可知AD=CE,DC=EA,根据“SSS”可求得△DEC≌△EDA;
(2)根据勾股定理即可求得
试题解析:(1)由矩形的性质可知△ADC≌△CEA,
∴AD=CE,DC=EA,∠ACD=∠CAE,
在△ADE与△CED中
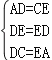
∴△DEC≌△EDA(SSS);
(2)∵∠ACD=∠CAE,
∴AF=CF,
设DF=x,则AF=CF=4﹣x,
在RT△ADF中,AD2+DF2=AF2,
即32+x2=(4﹣x)2,
解得;x=![]() ,
,
即DF=![]() .
.
-
科目: 来源: 题型:
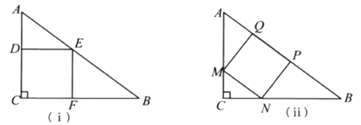
查看答案和解析>>【题目】一块直角三角形的木板,它的一条直角边AC长为1.5米,面积为1.5平方米.现在要把它加工成一个正方形桌面,甲、乙两人的加工方法分别如图(ⅰ)、(ⅱ)所示,记两个正方形面积分别为S1、S2,请通过计算比较S1与S2的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(a+b)x2+2cx+(b-a)=0,其中a、b、c分别为
 三边的长.
三边的长.(1)如果
 是方程的根,试判断
是方程的根,试判断 的形状,并说明理由.
的形状,并说明理由.(2)如果方程有两个相等的实数根,试判断
 的形状,并说明理由.
的形状,并说明理由. (3)如果
 是等边三角形,试求这个一元二次方程的根.
是等边三角形,试求这个一元二次方程的根. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=﹣
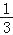 x+1与y轴交于点D.
x+1与y轴交于点D.
(1)求抛物线的解析式;
(2)证明:△DBO∽△EBC;
(3)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的P点坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(1,a)是直线y1=2x与双曲线y2=
 在第一象限的交点.
在第一象限的交点.(1)求双曲线的解析式;
(2)直接写出当y1>y2时,自变量的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列给出的条件中,能判定四边形ABCD为平行四边形的是()
A.AB=BC,CD=DAB.AB//CD,AD=BC
C.AB//CD,∠A=∠CD.∠A=∠B,∠C=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在RtΔABC中,∠C=90°,∠BAC的角平分线AD交BC边于D,以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D,与AB边的另一个交点为E.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为4,∠B=30°.求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.

相关试题

